Irrational & Rational Inequality (Example Problem)
Loading...
In addition to the same value that uses the "=" sign, there are also forms of inequality whether it is more than a value or less. Usually use the signs ">,
This lesson on inequalities is very important to understand so that when answering related questions it will be easier.
List of contents
Definition of Inequality

Before discussing in detail about the types of inequalities, you must first know what the term means.
In mathematics, it is described as a statement that explains the existence of a comparison between two or more elements or objects.
It can also be referred to as an explanatory sentence of two different statements. Some use less or more symbols, but they can also use less than or more than symbols.
Read: Math Comparison
Rational Inequality

This type of inequality uses numbers as fractions. It could be that both the numerator and denominator have their own variables, or it could be that only the denominator has a variable.
The general form commonly used for its description is:
> 0 or; g(x) 0
< 0 or; g(x) 0
To express a rational inequality, there are steps that need to be done. Starting from stating it in general form, then determining the generator of zeros that exist in the numerator and denominator.
Then the zero generator, will be written on a number line by specifying the appropriate sign at each interval.
If so, all you have to do is determine where the solution is. If it is stated that it is greater than or equal to, then the completion interval is in the positive part, while if the result is small or small equal to then the location of the interval is the negative part of the area solution.
There are two things that should not be done, the rational inequality will certainly be different from the irrational inequality, namely:
- Cross out the same factor or function, both in the numerator and denominator
- Doing cross multiplication
Does this inequality have any kind? It turns out that there are four with their own characteristics:
- Linear Quadratic Rational Inequality
- Quadratic Rational Inequality
- Linear Rational Inequality
- Absolute Rational Inequality
Read: One Variable Linear Inequality
Examples of Rational Inequality Problems

To make it clearer and clearer, you need to see firsthand what the examples of statements that contradict this irrational inequality look like.
Example Question 1
What is the result of the inequality:
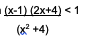
The answer is:
Step 1= change the left side to zero
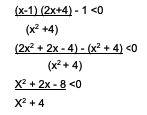
X2 + 4 is a positive definite, so that the focus is only on the numerator to be:
x2 + 2x – 8 <0
(x+4)(x-2) <0
It is found that the critical point of x is at -4 and 2
Step 2= create a number line with the solution area using the critical point
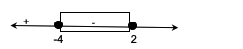
Step 3=determine the solution set which is {x|-4< x < 2}
Example Question 2
3x +5x – 3 5
What is the solution set?
Advertisement
Step 1:
3x + 5x – 3 5
3x + 5x – 3 – 55 – 5
3x + 5x – 3 -50
Step 2:
Equating the denominator of the inequality:
3x+5-5(x-3)x-3 0
3x+5-5x+15X-3 0
-2x+20x-3 0
Step 3:
Moving the sides of the numerator and denominator
-2x + 20 = 0
20 = 2x
x = 10
x-3 = 0
x =3
By knowing the value of x, where do you need to know again where the position of each value is with reference to g (x) 0
The thing to remember is, so that it must be replaced with zero so that the solution set becomes x < 3 U x 10
Read: Linear Inequality of Two Variables
Irrational Inequality
What is meant by irrational inequality is that the inequality with the forming function is in the root sign. It can be on the left or right side, it can also be a root function on both sides of the inequality.
Another meaning is, when the number in the inequality is a natural number then the value under the root is
The main way to find the result of an inequality is to find the square of each side. Then collaborated with algebraic formulas for predetermined intervals.
The general form of is:
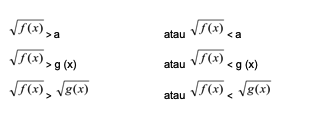
To solve this inequality, it takes some proper understanding, so that the result is not wrong.
- Make sure to first change the inequality to a general form, where on the left side it is made in the form of roots
- First determine the value on the right side of the inequality, with the following conditions:
a. If the value is zero or positive
- The right-hand side is zero or a positive number, then you need to solve the result of the two sides that have already been squared
- Finding solutions to irrational inequalities according to values that can satisfy the conditions for numbers under the radical sign
- Looking for slices when the solution is complete
b. If the value is negative
- Find the solution to the right-hand side inequality < 0
- Find the solution to the value under the root
- Find a value that can satisfy the conditions for the number below a
c. If the value is greater than or equal to zero
- Make the description for the right-hand side be < 0 or 0
- If the right hand side < 0, then look for the result first, then look for the result for the next section
- Combine the results of the solution into a complete irrational inequality.
Examples of Irrational Inequality Problems

As with rational inequalities, you also need to practice solving problems related to irrational inequalities. So that you will understand more about this type of inequality.
Example Question 1
What is the solution set for the inequality?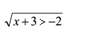
Answer:
x + 3 0
x≥ -3
The solution set is {x≥ -3}
Example Question 2
What is the solution set of 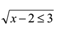
Answer:
The main condition is x-2≥ 0
Then it is changed to x≥2
Then square both sides to x – 2 9 which simplifies to x 11.
It's time to draw a finishing line with reference to the last result obtained.
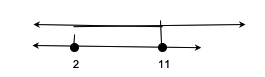
So we can conclude that the solution set is {x|2 x 11}
Conclusion
From the explanation above about rational inequalities and irrational inequalities, it can be concluded that both have different characters.
The rational type has characteristics, namely fractional numbers with a numerator and denominator that must be translated and of course the result cannot be equal to zero.
While irrational deals with numbers under the root sign, where the inequality cannot be equal to zero.
To be able to solve various problems, understanding of both must be really maximal so that the results are not wrong. You also need to understand the equation of a line, which will explain the solution set for each inequality.
Already understand all about irrational and rational inequalities? I hope you can understand all of the information above and use it as a reference for working on problems related to inequalities.
X CLOSE
Advertisements
ADVERTISEMENT
X CLOSE
