Quadrilateral Pyramids: Formulas, Nets, Sample Problems
Loading...
Build a space named pyramid has 4 types which are distinguished based on the shape of the base. The focus of this discussion is the type of pentagon pyramid whose base is a pentagon. While the other 3 types are triangular pyramids, quadrangles and hexagons.
Not only as a lesson in school, building pyramids turns out to have important uses in human life. The following explanation will discuss starting from formulas, sample questions to the application of pentagons.
List of contents
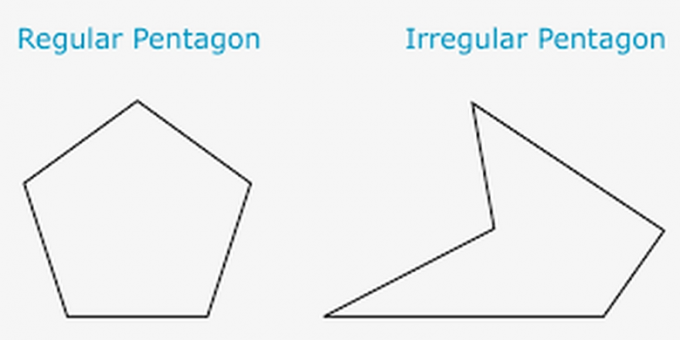
Definition of a pentagon
A pentagon pyramid is a type of pyramid that has a base in the form of a pentagon, both regular and arbitrary pentagons. This type of pyramid with a pentagon base is also built from the side of a blanket that has a triangular shape.
While the pentagon is a type of flat shape that has 5 sides as a barrier. The large number of sides causes this flat shape to be called a pentagon.
Read: Pyramid Formula
Examples of Application of the pentagon

In everyday life, some of the uses of a pentagon pyramid include making tents, designing wheel mounts for airplanes, constructing garbage collectors, designing roofs and hat.
How about a pentagon? This flat shape is not only applied to pyramids, but also to other types of shapes, for example a pentagon prism. The point is, to build a space that requires a base with many sides, you can use a pentagon flat shape.
pentagon
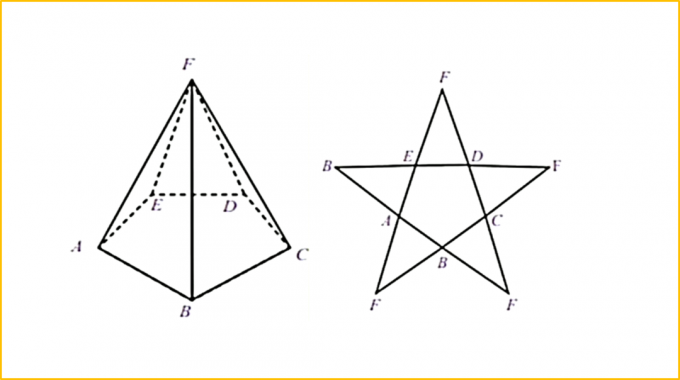
What does a pyramid look like with a pentagon base? Here's the picture:

It can be seen in the figure that the base of the pyramid is formed from a pentagon whose sides include sides AB, BC, CD, DE and AE. However, it should be noted that the 5 sides are only owned by the pentagonal shape, not the total number of sides of the pyramid.
The shape of a pentagon pyramid has 6 sides consisting of five upright sides of the pyramid and one side of the base which is a flat shape. It is clear in the picture above that there are five upright sides that form a triangle.
Read: Geometry
Characteristics of a pentagonal pyramid

Each type of pyramid has its own characteristics that make it unique and different from other types. The following are the characteristics of this type of pyramid whose base is a pentagon:
- There are 6 sides which include 5 sides of the blanket with a triangular shape and 1 side of the base with a flat pentagon shape;
- There are vertices whose sum is 6;
- There are 10 ribs which include 5 ribs on the base and 5 ribs on the sides of the pyramid blanket.
Pyramid Nets
All spatial shapes have nets which are the result of division or overhaul of these shapes. When webs whose parts are interconnected are combined, they will form a complete spatial structure.
This type of pyramid building with a base in the form of a pentagon certainly has nets that look as follows:
Seen in the picture, the webs adjacent to the pyramid are intact. So, when the pyramid is dismantled, the pattern of the nets will be seen.
It can be seen clearly that there are 6 sides that make up the pyramid. The base is clearly visible in the form of a flat pentagon and the upright side is a triangle.
Read: Pyramid Hexagon
Volume Formula of a pentagon pyramid
How to calculate the volume of a building must be based on a special formula. The following is the formula for the pentagonal pyramid used to determine the volume of this type of pyramid:
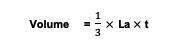
Formula description:
The area of the base (La) refers to the area of the base owned by the pyramid
Height (t) refers to the size of the height possessed by the pyramid
Example of a pentagon pyramid
It's time to further sharpen your understanding of the material for building a pyramid based on a pentagon by looking at some of the sample questions below:
1. There is a pentagonal pyramid that has a height of 20 cm. The area of the base of the building is 45 cm2. Determine what the volume is!
Advertisement
From the question it is known that:
t: 20 cm
base area: 45 cm2
The next step is to enter these numbers into the formula so that the calculation becomes:
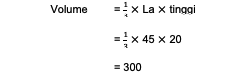
Thus, the volume of the figure is 300 cm3.
2. Bayu made a pentagonal pyramid shape for the roof of the pet cage he had. The pyramid is 9 cm high with a base area of 15 cm2. Then, what is the volume of the pyramid for the roof?
Based on the problem, it is known that t = 9 cm and the area of the base = 15 cm2. So, the next step is to directly calculate the volume of the pyramid with the following formula:
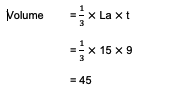
In conclusion, the volume of the pyramid created by Bayu is 45 cm3.
3. A rectangular pyramid has a volume of 120 liters. After being measured, the pyramid is 15 dm high. Calculate the area of the base that forms the shape of the space!
In the problem, it is known that v = 120 liters and t = 15 dm. The calculation still uses the formula for the volume of the pyramid by positioning the area of the base as the question asked. So, the calculation process is like this:
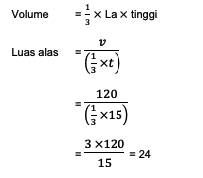
Based on these calculations, the area of the base of the building is known to be 24 dm .2.
4. There is a pentagon whose volume is 50 cm3. In addition, the area of the base is also known, which is 25 cm2. The only unknown component is height. Try to count how high the pyramid is!
Known from the question:
Volume (v): 50 cm3
Base area: 25 cm2
Tall: ?
Just as before finding the area of the base of the pyramid, the calculation for finding the height of the pyramid is also still based on the basic formula for a pentagonal pyramid. Here's how to calculate it:
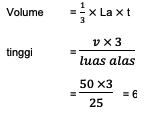
So, the height of the pyramid in question is 6 cm.
5. Two pentagonal pyramids have each size. Pyramid A has a height of 30 cm and a base area of 40 cm2. While pyramid B is known to be 25 cm high and the base area is 35 cm2. What is the total volume of the two pyramids?
It is known from the following questions:
t (lima A): 30 cm
area of the base (pyramid A): 40 cm2
t (lima B): 25 cm
base area (lima B): 35 cm2
Now, let's jump right into the volume formula. First calculate the volume of the pyramid A:

Then, calculate the volume of pyramid B, namely:

The question of asking about the total volume of the two shapes, then the way is simply to add:
Total volume = volume of pyramid A + volume of pyramid B
= 400 cm3 + 291.67 cm3
= 691.67 cm3
A pentagon pyramid is a type of pyramid that is formed from a base in the form of a flat pentagon and a triangular upright side. The whole side that is owned by the wake of the space as much as 6 pieces. In its application, this type of pyramid is often used as a building roof.
X CLOSE
Advertisements
ADVERTISEMENT
X CLOSE
