Juring and Teams: Definition, Formulas, Example Problems

July 01, 2022
InMiscellanea

click fraud protection

Flat shapes that are very easy to recognize are called circles. There are no corner points on the circle, but the flat shape has several elements, one of which is a segment which is further divided into several types.

Other elements possessed by a circle are chord, center, radius, diameter, arc, arc and apothem. The discussion this time will focus on the elements of categories and sections which include definitions, formulas and examples of questions.

List of contents

What Are Clashes and Slices?

Each element in the circle has a meaning that distinguishes one another. The definition of a segment is an area inside a circle that is flanked by 2 other elements, namely the arc and the bowstring.

This element is divided into 3 types which are distinguished based on the amount of area they have. The following is an explanation of the 3 types:

instagram viewer

1. Little Friends

It is called a small segment because the circle element has an area that is less than the area of a semi-circle. The circular bow and bowstring are the boundaries of this area.

2. Half Circles

Furthermore, the semicircle is the element in the circle that has an area equivalent to the area of the semi-circle.

3. Big Group

The definition of a large tembeng is an element of a circle that has a larger area than the small type. In a circle, this type is the area bounded by the arc of the circle and the chord.

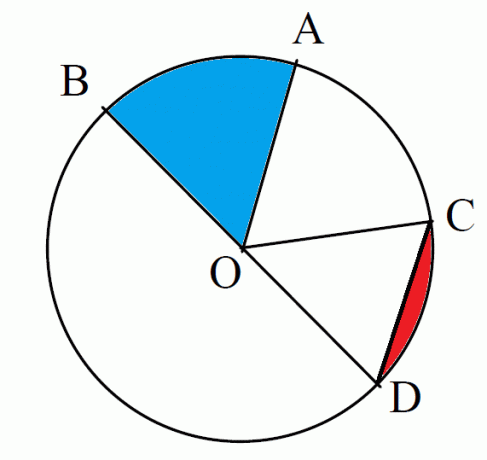
The following is an example of an image of a group and an entire circle to make it easier to recognize and distinguish each element:

Next, what is meant by juring? A circle is one of the elements of a circle whose area is flanked by the arc and the radius of the circle. This area is divided into 2 types, namely large and small areas.

The area called the small cross is marked by the small arc of the circle and the radius that becomes the flanks. While the large area is flanked by a large arc of a circle and its radius.

Read: Slice of Two Circles

Circle Surge Formula

In mathematics, the area of a square is calculated by dividing the quotient of the central angle by 360 .⁰, then multiplied by the area of the circle. The following formula is used:

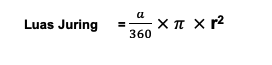
Formula description:

In its application, there are problems that are easy to solve so that the known numbers can be directly entered into the formula. However, there are also complex types of questions that require a longer completion process before arriving at the formula.

It should be noted that the area of the section is closely related to the calculation of the segments. Because, the result of the area of the circle is used in the formula to calculate the area of the circle element.

Read: Circle Equation

Circle Tensile Formula

The way to calculate the segment is to find the difference between the area of a triangle and the area of a triangle. Therefore, it is necessary to calculate the area of the two areas in order to enter the formula for calculating the area of the cluster.

The formula used is:

It is necessary to analyze the questions well and do the calculations carefully because the process is quite long. Even so, calculating clusters is still relatively easy if you have found the numbers that must be entered into the formula.

Read: Pie Chart

Examples of Juring and Team Problems

Here are some examples of questions to hone skills in the material of the elements of a circle, especially crosses and segments.

1. Example of Juring

What is the area of a circle if a circle has a radius of 10 cm and an angle at the center of the circle whose measure is 60 .?⁰?

The solution:

From the problem, it is known that r = 10 cm and a = 60⁰

So, just put these numbers into the formula to find out the area of the square element:

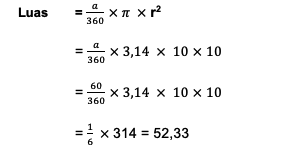
Based on these calculations, it can be seen that the area of the circle on the circle is 52.33 cm².

A circle has a radius of 9 cm and a central angle of 90⁰. Try calculating the area of the square based on these data!

From the problem, it is known that r = 9 cm and a = 90⁰, so that we can immediately proceed to the use of the area formula, namely:

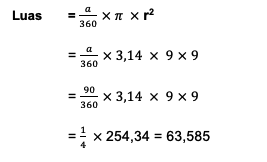
So, it is clear that the area of the cross-section in the circle is 63,585 cm².

Circle A has an area of 770 cm² and a radius of 35 cm. Based on these data, determine the angle of the cross!

It is known that r = 35 cm and the area of the slit = 770 cm². The value used for this calculation is so that it is easier. The formula used is:

Based on these calculations, the angle of the net is 72⁰

2. Example of Team Problems

A circle has a radius of 21 cm and an angle of 60 .⁰. So, how much area is there in the flat figure?

Before entering into the core formula, it is necessary to first find the area of the area using the following formula:

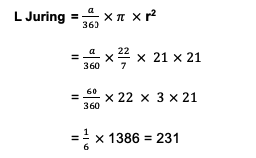
So, the area of the slit in a circle is 231 cm². After that, it's time to calculate the area of the triangle with the formula below:

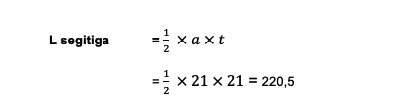
Now, the area of the triangle is 220.5 cm²

Next, enter these numbers into the core formula to calculate the area of the cluster, namely:

= Area of the square – area of the triangle

= 231- 220,5

10.5 cm²

Thus, it is known that the area of the segment on the circle has an area of 10.5 cm².

Circle A has a chord 20 cm long. Find the area of the segment on the circle!

The first step is to calculate the radius of the circle. The triangle formed in the circle is an isosceles right triangle whose hypotenuse is 20 cm long and the angle is 90 .⁰. The calculation of the radius is:

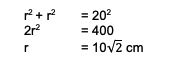
So, the radius of the circle is 10 cm or the same as 200 cm. The next step is to find the area of the square and the triangle in the circle:

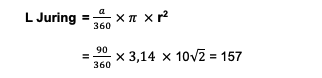
So, the area of the square in a circle is 157 cm². Next, calculate the area of the triangle. It is known that the base and height of the triangle are the same as the radius of the circle, which is 200 cm.

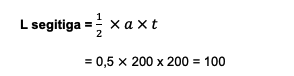
Thus, the area of the triangle has an area of 100 cm²

The last step is to calculate the area of the segment by finding the difference between the area of the square and the triangle.

The area of the square – the area of the triangle = 157 – 100 = 57 cm²

Finally, it can be seen that the area of the circle is 57 cm .²

The two elements of a circle, namely segments and sections, which have just been discussed, have calculations that are fairly easy if you pay close attention to the questions. These elements are also related because the area of the intersection is used to determine the area of the segments on the circle.

X CLOSE