KIRCHHOFF'S LAW 1 & 2: Inventors, Formulas, Example Problems

Kirchhoff is one of the physicists who provided services in the science of electricity. He is famous for Kirchhoff's Laws I and II. It was discovered by a person whose full name is Gustav Robert Kirchhoff, a German physicist.

This law is one of the laws in electronics which has a function to analyze the current and voltage in the circuit. Introduced by Kirchhoff for the first time in 1845, it consists of two laws.

Gustav Robert Kirchhoff

His full name is Gustav Robert Kirchhoff, is a German physicist who was born on March 12, 1824 in Konigsberg, Prussia. He died on October 17, 1887, at the age of 63, in Berlin, Germany.

Kirchhoff's mother is Johanna Henriette Wittke, while his father is Friedrich Kirchhoff who is a lawyer. Kirchhoff married Clara Richelot in 1847, they had three sons and two daughters.

After Richelot died in 1869, Kirchhoff remarried to Luise Brommel in 1872. Spending part of his life as a professor and professor of physics, Kirchhoff contributed to the circuit law formulas for electrical engineering in 1845.

In addition, Kirchhoff also contributed to discovering the law of thermal radiation or often known as thermodynamics (1859-1861), and spectroscopy. In addition, of course Kirchhoff's Law is one of his contributions as well.

Read: Electron Configuration

Kirchhoff's Law 1

This law is known as the junction rule or the law of branching, where the law fulfills the conservation of charge; A multi-switch circuit is required which contains branching points when the current is divided.

When the state is constant, there is no accumulation of electric charge at any point in the circuit, so the amount of charge entering at each point will leave that point again with the same amount. How does Kirchhoff's First Law sound?

"The amount of electric current that flows into a point to a junction or node is the same as the amount of electric current that comes out of that point."

Simply put, this law talks about the current that exists at the junction of a closed circuit. The basis of this law is the Law of Conservation of Charge with the sound "The charge at a point A is the same as the charge at point B", in the absence of an external force acting.

Kirchhoff's Law Formula 1

Mathematically, Kircchoff's First Law is stated as follows.

I_enter = I_{go out}

Kirchhoff's 2nd Law

This law is also known as the loop rule or loop rule, because originally the potential difference at two branching points in a circuit is constant. This law also proves the existence of the Law of Conservation of Energy.

If the charge Q at any point has a potential V, then the energy of the charge is QV. Next, as charge moves across the loop, the existing charge gains or loses energy as it passes through the battery resistor or other element.

However, when it returns to the starting point again, the energy of the charge returns to QV again. Kirchhoff's 2nd Law reads as follows.

"The sum of all the voltages around a closed loop in a circuit is equal to zero."

Kirchhoff's second law itself aims to measure the voltage potential difference that exists in a circuit that has no branches.

Read: Electrical circuits

Kirchhoff's Law Formula 2

Mathematically, Kirchhoff's II Law is stated as follows.

+ IR = 0

In addition to the formula, there are a number of rules that you should pay attention to from this law. First determine the direction of the loop in the circuit, then apply the following points.

• The voltage drop (SIR) will be positive (+) if it is in the direction of the loop.
• The voltage drop (SIR) will be negative (-) if it is in the opposite direction to the loop.

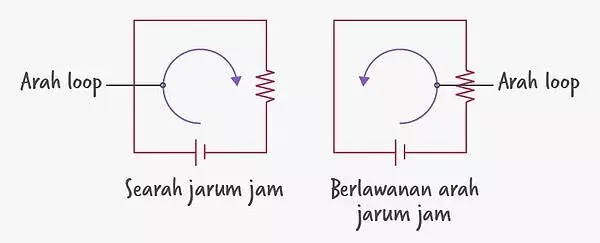
• The electromotive force (SE) will be positive (+) if it meets the positive pole of the voltage source.
• The electromotive force (SE) will have a negative sign (-) if it meets the negative pole of the voltage source.

Read: Ionic Bond

Example of Kirchhoff's Law Problem

So that you can better understand how Kirchhoff's Laws I and II are applied in several model questions, you can practice and try to answer and understand the discussion of the following examples of questions.

1. Example Question 1

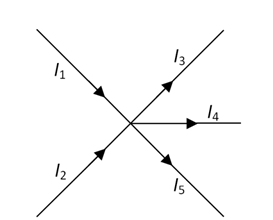
It is known, a circuit has a strong current as follows. Determine the correct mathematical form of the circuit!

Solution:

2. Example Question 2

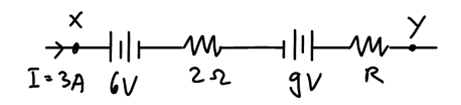
Given, the following circuit, having an electric current of 3 A, flows from X to Y with a potential difference between X and Y being 12. How much is the resistance?

Solution:

3. Example Question 3

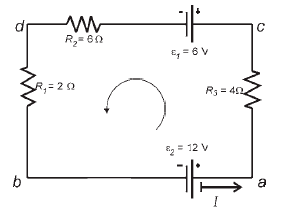
There is an electrical circuit as follows. Using Kirchhoff's second law, how much electric current is there in the circuit?

Solution:

4. Example Question 4

Consider the following electrical circuit diagram. If it is known₁ = 16 V; ɛ₂ = 8 V; ɛ₃ = 10 V; R₁ = 12 ohms; R₂ = 6 ohms; and R₃ = 6 ohms, what is the magnitude of the electric current I?

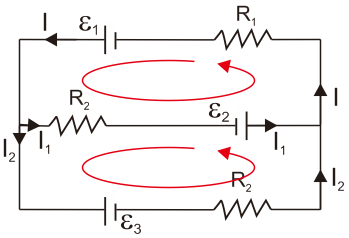
Solution:

Have you understood all the explanations of Kirchhoff's Law above? Especially for the second law, don't make a mistake in determining the direction of the loop so that the resulting answer is not wrong. Happy practicing again with questions from various sources!