Mean, Median, Mode (Understanding, Formulas, Questions)

June 26, 2022
InMiscellanea

Often we are faced with situations that require us to determine the mean, median, or datum with the most frequency. In determining these three things, there is the mean, median, and mode that can help us solve them.

Therefore, let's study the mean, median, mode through this article, so that we don't experience difficulties when facing this situation. Have a good study!

List of contents

Definition of Mean, Median, and Mode

1. mean

The mean or average is representative of a large set of data. The mean is denoted by x̄ (read as x bar) and the value can be calculated from single data or single data in groups.

2. median

The median (Me) or quartile is the middle value of the data set after the data is sorted from smallest to largest. If a data set has an odd number, then the median lies on the data 1/2(n+1) with n as the number of data.

instagram viewer

However, if a data set has an even number, then the median lies at and data n/2 and data (n/2) + 1 is the number of data.

3. mode

The mode (Mo) is the datum that appears frequently and becomes a measure of concentration to express the phenomenon with the most frequency.

If the data obtained is single data in groups or data presented in tables, then you can immediately see the datum with the most frequency.

Read: Math Limits

Application of Mean, Median, and Mode

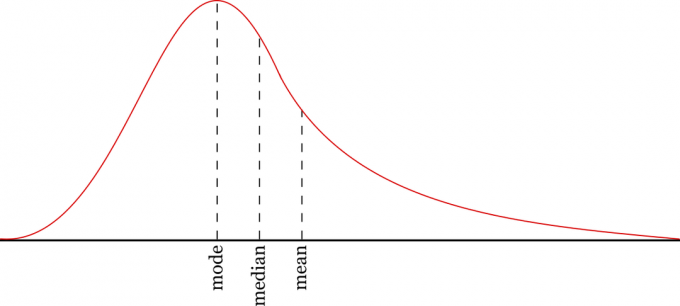
The mean, median, mode are usually required to analyze the results or collect data. After the data is successfully obtained, then the data will be processed using statistical methods.

For example, when getting data related to rice yields every year. The average or mean can be used to determine how many tons of rice are produced per year on average. Meanwhile, the median is used if you want to find the middle value of the harvest.

The mode is used to find out how many tons of rice are obtained in a certain amount or to determine the frequency at which most of the total rice yields are harvested.

For more details, let's learn the formulas of mean, median, mode!

Mean, Median, and Mode Rumus Formulas

Mean Formula

1. Single Data

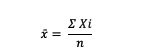
x̄ = average value (mean)

Xi = sum of the i-th data values

n = number of data

2. Grouped Data

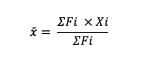
x̄ = average value (mean)

Fi = frequency of the i-th data group

Xi = the mean value of the i-th data group

Read: Math Derivatives

Median Formula

1. Single data with odd number of datum

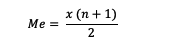
In determining the median if the datum has an odd number, you can use the following formula:

Me = median

x = datum

n = number of data

2. Single data with even datum

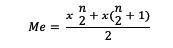
If the datum turns out to be an even number, use the following formula to determine the median:

Me = median

x = datum

n = number of data

3. Grouped data

Me = median

tb = lower edge of median class

n = number of data

Fkum = cumulative frequency before median class

Fi = median class frequency

k = class length

Mode Formula

In determining the mode on a single data, you can create a frequency table to make it easy to see the highest frequency in each datum. While for grouped data, you can use the formula below:

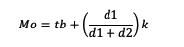
Mo = mode on grouped data

tb = lower edge of mode class

d1 = frequency of the mode class minus the frequency of the previous class

d2 = frequency of the mode class minus the frequency of the next class

k = class length

Read: Logarithm

Examples of Mean, Median, and Mode Problems

After finishing with the mean, median, less mode afdol it feels like if you haven't practiced that understanding with practice questions. Let's do the following questions!

1. The numbers are 163, 167, 168, 170, 175, 180, 185. What is the median value?

Answer:

163, 167, 168, 170, 175, 180, 185

So, the median value of the series of numbers is 170 (B)

2. Pay attention to the following table!

Score	Frequency
105	5
95	2
80	3
75	1
65	1
60	2

The values that often appear from the table above are?

Answer:

Seen from the table, the value with the highest frequency is 105 (A)

3. The numbers are 150, 165, 168, 168, 175, 177, 180, 188. What is the median value?

188
175
165
171,5
177

Answer:

150, 165, 168, 168, 175, 177, 180, 188

Use the formula:

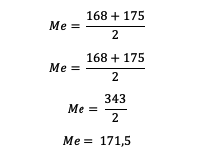
So, the median value of the series of numbers is 171, 5 (D)

4. The mode values of 40,40,45,45,45,50,55,65,65,70 are …

Answer:

Number	Frequency
40	2
45	3
50	1
55	1
65	2
70	1

The mode or value with the highest frequency of these numbers is 45 (E)

Look at the following table to answer questions number 5, 6, and 7!

Score	Frequency
10-20	2
21-31	8
32-42	15
43-53	7
54-64	10
65-75	3

5. What is the mean of the above data?

41,77
41,87
42,77
42,87
43,77

Answer:

Score	Frequency	Fkum	Xi	Fi. X.Xi
10-20	2	2	15	30
21-31	8	10	26	208
32-42	15	25	37	555
43-53	7	32	48	336
54-64	10	42	59	590
65-75	3	45	70	210

Question Mean Median Mode no 5 So, the mean or average value of the data is 42.87 (D)

6. What is the median of the table above?

40,27
40,37
40,47
40,57
40,67

Answer:

Score	Frequency	Fkum	Xi	Fi. X.Xi
10-20	2	2	15	30
21-31	8	10	26	208
32-42	15	25	37	555
43-53	7	32	48	336
54-64	10	42	59	590
65-75	3	45	70	210

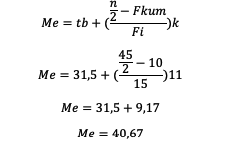Question about mean median mode no 6 So, the median of the above data is 40.67 (E)

7. What is the mode of the above table?

35,53
35,63
36,63
36,53
36,73

Answer:

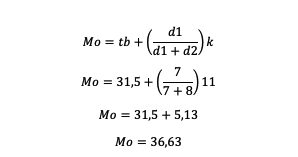
Answer:

The mode value obtained is 36.63 (C)

Conclusion

In statistics, there are single data and group data. We can find the mean, median, mode of single data or grouped data using the formulas described above.

As already explained, the mean is the average or representative of the data. The mean is the middle value of a data. While the mode is the datum that appears most often or has the most frequency.

In everyday life, we apply a lot of mean, median, mode to help solve these problems. So, it is important for us to understand this material well.

Well, that's all the discussion about the mean, median, mode that can help your daily problems. Don't forget to always practice with the existing questions you can become even better.

X CLOSE