Flat Shapes: 8 Kinds, Formulas, Properties, Example Problems, Understanding
Based on what is mentioned by wikipedia, flat shapes are a term for various two-dimensional shapes.
Flat shapes include: circles, rhombuses, kites, trapezoids, parallelograms, triangles, rectangles and squares.
Each of these shapes has a formula to calculate the area as well as the circumference that differs from one shape to another. For more about flat fields, take a good look at the reviews below.
Table of contents
Two-dimentional figure
Completing the description above, a flat shape is a part of a flat plane bounded by straight or curved lines.
The definition itself in detail is: a shape that has a flat surface and has two dimensions, namely length and width but does not have height and thickness.
Thus, the short definition of flat shape is abstract.
Flat Build Formula
In the following, we will give the types or types of flat shapes and their properties. Check out the reviews below.
1. Square
Definition of Square
A square is a 2-dimensional flat shape formed by 4 edges with the same length and 4 right angles.
A square can also be called a flat shape that has equal sides and equal angles.
Square Properties
- All of its sides are the same length and all opposite sides are parallel.
- Each of the angles it has is a right angle.
- It has two diagonals of the same length and intersect in the middle and form a right angle.
- Each of the angles is bisected by the diagonal.
- It has four axes of symmetry.
The formula in Square
The following are some of the formulas commonly used in rectangular shapes, including:
The formula for the area of a square, namely:
L = S x S
The formula for the perimeter of a square is:
K = S + S + S + S or K = 4 x S
Information:
- L: Area
- K: Around
- S: Side
Problems example:
Look at the picture below:
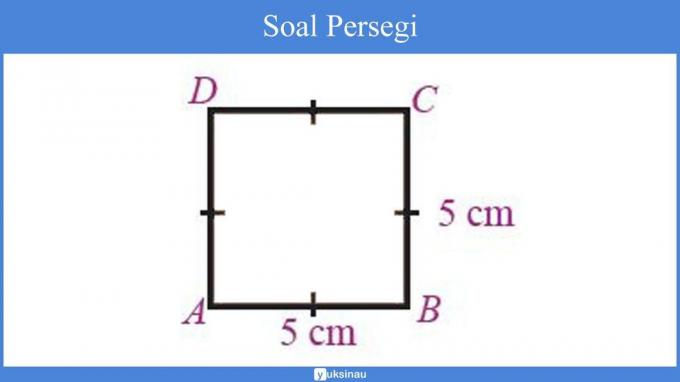
From the figure above, determine:
a. Determine the area of the square:
b. Determine the perimeter of the square:
Answer:
a. The formula for the area of the square ABCD is: s x s, so that
= 5 cm x 5 cm
= 25 cm2.
So, the area of the square ABCD is: 25 cm2.
b. The formula for the perimeter of the square ABCD is: 4xs, so that
= 4 x 5 cm
= 20 cm.
So, the total perimeter of the square ABCD is 20 cm.
2. Rectangle
Definition of Rectangle
A rectangle is a 2-dimensional flat shape formed by 2 pairs of long and parallel ribs and has 4 right angles.
Properties of Flat Rectangles
- Each of the opposite sides has the same length and is also parallel.
- All angles are right angles.
- It has two diagonals that are the same length and intersect at the center of the rectangle. The point is to bisect the diagonals of the same length.
- It has two axes of symmetry, namely the vertical axis and the horizontal axis.
The formula in the Flat Shape Rectangle
The formula for the area of a rectangle is:
L = p x l
The formula for the perimeter of a rectangle is:
K = 2 x (p + l)
Information:
- L: Area
- K: Around
- p: long
- l: width
Problems example
A rectangular shape, having p = 10 cm and l = 5 cm, consists of EFGH:
Question:
a. Calculate the area of the rectangle EFGH:
b. Find the perimeter of the rectangle EFGH!:
Answer:
a. The formula for the area of the rectangle EFGH is L= p x l, so that
L = 10 cm x 5 cm
L = 50 cm2.
So, the area of the rectangle EFGH is 50 cm2.
b. The formula for the perimeter of the rectangle EFGH is: 2 x (p + l), so that
= 2 x (10 cm + 5 cm)
= 2 x 15 cm.
= 30 cm
So, the perimeter of the rectangle EFGH is 50 cm.
3. Triangle
Definition of Flat Triangle
A triangle is a 2-dimensional flat shape formed by 3 straight lines and 3 angles.
So that a flat figure formed from three or more straight lines is called a triangle.
The Nature of the Flat Triangle
- In a triangular structure, all three angles have a measure of 180º. (if you add up the result is 180)
- A triangle has 3 sides and 3 vertices.
The formula in the Triangle Flat Shape
The formula for the area of a triangle is:
Area = x a x t
The formula for the perimeter of a triangle is:
Perimeter = s + s + s or K = a + b + c
Problems example
A triangle has a size as shown in the figure below:
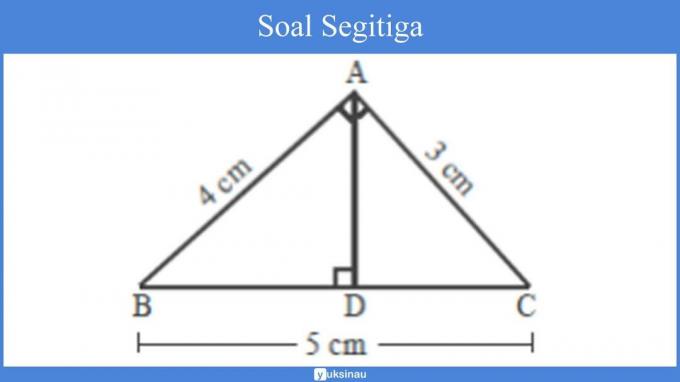
Question:
a. Calculate the area of the triangle:
b. Calculate the perimeter of the triangle:
Answer:
a. The area of a triangle The formula is x a x t, so that
= x 3 cm x 4 cm
= x 12 cm2.
= 6 cm2
So, the result of calculating the area of a triangle is 6 cm2.
b. The perimeter of the triangle is = s + s + s, so
= AC+AB+BC
= 3cm+4cm+5cm
= 12 cm.
So, the perimeter of the triangle is 12 cm.
4. Parallelogram
Definition of Flat Shape Parallelogram
The definition of a parallelogram itself is a 2-dimensional flat shape formed by 2 pieces pairs of ribs, each of which is the same length and parallel to her partner.
Then the parallelogram has 2 pairs of right angles where each angle is equal to the angle in front of it.
Nature of Flat Build Parallelogram
- The properties of a parallelogram do not have folding symmetry.
- Parallelograms have a second degree of rotational symmetry.
- Opposite parallelogram angles have the same size.
- A parallelogram has 4 sides and 4 angles.
- Its diagonals have unequal lengths.
- Parallelogram has 2 Pairs of Sides which are parallel and the same length.
- A parallelogram has 2 obtuse angles and 2 acute angles.
The formula in Build Flat Parallelogram
| Name | Formula |
| Roving (Kll) | Kll = 2 × (a + b) |
| Area (L) | L = a × t |
| Side of Base (a) | a = (Kll 2) – b |
| Oblique Side (b) | a = (Kll 2) – a |
| t is known L | t = L a |
| a is known L | a = L t |
Problems example
Look at the image of the parallelogram ABCD below!
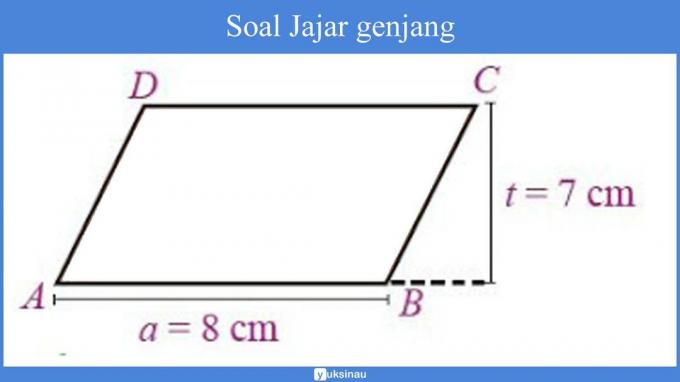
Length BC = DA = 8 cm.
Question:
a. Find the area of the parallelogram ABCD, which is:
b. Find the perimeter of the parallelogram ABCD, which is:
Answer:
a. The area of the parallelogram ABCD is = a x t, so that
= 8 cm x 7 cm
= 56 cm2
So, the area of the parallelogram ABCD is 56cm2.
b. The perimeter of the parallelogram ABCD is s + s + s + s, then:
K = AB + BC + CD + DA, that is:
K = 8cm + 8cm + 8cm + 8cm
= 32 cm.
So, the perimeter of the parallelogram ABCD is 32 cm.
5. Trapezoid
Definition of Flat Trapezoid
The definition of a trapezoid itself is a 2-dimensional flat shape formed from 4 edges, 2 of which are parallel but not the same length.
But there is also a trapezoid whose third rib is perpendicular to its parallel ribs which is commonly known as a right-angled trapezoid.
Nature of Flat Build Trapezoid
- A trapezoid is a flat shape with 4 sides (quadrilateral).
- It has 2 parallel sides that are unequal in length.
- Has 4 corner points.
- At least in a flat trapezoid has 1 obtuse angle
- A trapezoid has 1 rotational symmetry.
The formula in Build Flat Trapezoid
| Name | Formula |
| Area (L) | 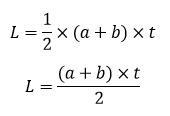 |
| Roving (Kll) | Kll = AB + BC + CD + DA |
| Height (t) |  |
| Side a (CD) |
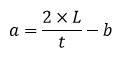 orCD = Kll – AB – BC – AD orCD = Kll – AB – BC – AD
|
| Side b (AB) |
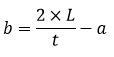 orAB = Kll – CD – BC – AD orAB = Kll – CD – BC – AD
|
| AD side | AD = Kll – CD – BC – AB |
| side BC | BC = Kll – CD – AD – AB |
Problems example:
Take a look at the EFGH trapezoid shape below!
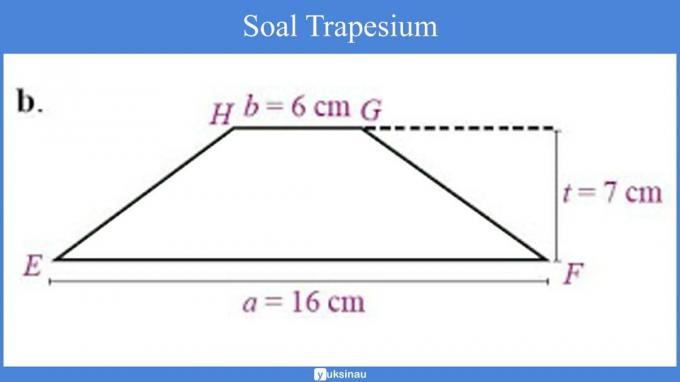
The length of EH = FG is 8 cm.
Question:
a. Find the area of the trapezoid EFGH:
b. Find the perimeter of the trapezoid EFGH:
Answer:
a. The area of the trapezoid EFGH is: x (a + b) x t then,
= x (16cm + 6cm) x 7cm
= x 22 cm x 7 cm
= 11cm x 7cm
= 77 cm2
So, the area of the trapezoid EFGH above is 77 cm2.
b. The perimeter of the trapezoid EFGH has the formula: s + s + s + s, then:
K = EF + FG + GH + HE
K = 16cm + 8cm + 6cm + 8cm
= 38 cm.
So, the area of the trapezoid EFGH above is 38 cm.
6. Kites
The definition of a kite itself is a 2-dimensional flat shape formed by 2 triangles isosceles and rectangular in shape which has a base that coincides and is shaped into a kite – kite.

Nature of the Flat Shape of Kites
- A kite is a flat shape with 4 sides (quadrilateral).
- Has 2 pairs of sides that form different angles.
Pair 1 is the sides a and b, forming the angle ABC.
Pair 2 is the sides c and d, forming the angle ADC. - It has a pair of opposite angles that are the same measure.
The angles BAD and BCD are opposite and have the same measure. - Has 2 diagonals of different lengths.
- The diagonals of the kite are perpendicular to each other (90º).
- The longest diagonal is the kite's axis of symmetry.
- Kites only have 1 axis of symmetry.
The formula that exists in Waking Up Flat Kites
| Name | Formula |
| Area (L) | L = × d1 × d2 |
| Roving (Kll) | Kll = a + b + c + d |
| Kll = 2 × (a + c) | |
| Diagonal 1 (d1) | d1 = 2 × L d2 |
| Diagonal 2 (d2) | d2 = 2 × L d1 |
| a or b | a = (½ × Kll) – c |
| c or d | c = (½ × Kll) – a |
Problems example
Watch the ABCD kite below!
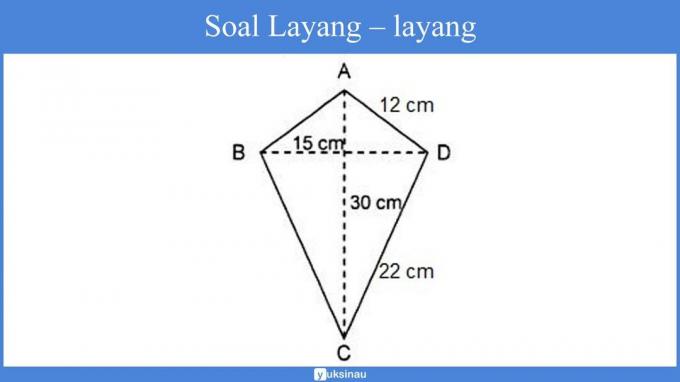
Is known;
Length BC = length CD
Length AB = length AD
Question:
a. Calculate the area of the kite ABCD!
b. Calculate the perimeter of the kite ABCD!
Answer:
a. The area of the kite ABCD is = x d1 x d2, so
= x AC x BD
= x 30 cm x 15 cm
= 225 cm2
So, the area of the kite ABCD is 225 cm2.
b. The perimeter of the kite ABCD is: 2 x (x + y), so
= 2 x (AB + BC)
= 2 x (12 cm + 22 cm)
= 2 x 34 cm
= 68 cm
So, the perimeter of the kite ABCD is 68 cm.
7. Cut the rice cake
A rhombus is a 2-dimensional flat shape formed by 4 sides of the same size length and has 2 pairs of non-angled angles with opposite angles having a measure of same.
In English, a rhombus is referred to as rhombus.
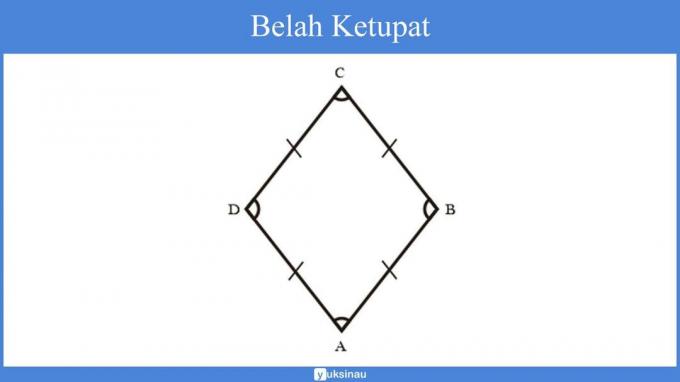
The nature of the flat shape of a rhombus
- All four sides are the same length.
- It has 2 diagonals that are perpendicular to each other.
Diagonal 1 (d1) and diagonal 2 (d2) in a rhombus are perpendicular to each other to form a right angle (90°). - The angles opposite each other have the same measure.
In a rhombus, opposite angles have the same measure. The illustration above shows the angle measure sudutABC = ADC and BAD = BCD. - The measure of the four corners is 360.
- It has 2 axes of symmetry where where is the diagonal.
- The rhombus has a level 2 Rotation Symmetry.
- It has 4 sides and 4 corners.
- The four sides of a rhombus have the same length.
The formula in the Flat Shape of a Rhombus
| Name | Formula |
| Roving (Kll) | Kll = s + s + s + s |
| Kll = s × 4 | |
| Area (L) | L = × d1 × d2 |
| side(s) | s = Kll 4 |
| Diagonal 1 (d1) | d1 = 2 × L d2 |
| Diagonal 2 (d2) | d2 = 2 × L d1 |
Problems example:
Check out the rhombus below!
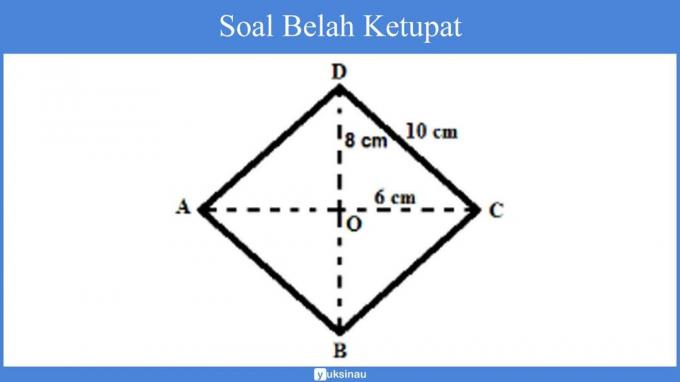
AC length is 12 cm
BD length is 16 cm
The question is:
a. Find the area of rhombus ABCD!
b. Find the perimeter of rhombus ABCD!
Answer:
a. The area of rhombus ABCD is = x d1 x d2, so
= x AC x BD
= x 12 cm x 16 cm
= 96 cm2
So, the area of rhombus ABCD is 96 cm2.
b. The perimeter of rhombus ABCD is: s + s + s + s, so that
= AB + BC + CD + DA
= 4 x s
= 4 x 10 cm
= 40 cm
So, the perimeter of rhombus ABCD is 40 cm.
8. Circle
Definition of Circle
A circle is a two-dimensional plane formed by the set of all points that are equidistant from a fixed point.

- Circle center (P): The fixed point on the circle is called the center of the circle.
- radius (r): the distance of another point on the center of the circle is called the radius of the circle
- Curve: The set of all points of the circle and then form a curved line that becomes the circumference of the circle.
- Diameter (d): the line drawn by the two points on the curve and passing through the center is called the diameter (d). The diameter of a circle has a length of 2 × r.
- phi (π): the value of the ratio between the circumference and diameter of a circle is always constant, namely 3.14159 (rounded to 3.14) or 22/7. This value is obtained from Perimeter ÷ Diameter = phi.
Characteristics of Flat Circles
- It has infinite rotational symmetry.
- It has infinite axis and folding symmetry.
- Has no corner points.
- Has one side.
| Name | Formula |
| Diameter (d) | d = 2 × r |
| radius (r) | r = d 2 |
| Area (L) | L = x r x r or L = x r2 |
| Roving (Kll) | Kll = x d |
| Looking for r | r = kll/ 2π |
| r = L/ |
Problems example
Finding Area
If it is known that a circle has a diameter of 14 cm. What is the area of the circle?
Answer:
Is known:
- d = 14 cm
Because d = 2 × r then:
r = d/2
r = 14/2
r = 7 cm
Asked:
- Area of circle?
Solution:
Area = × r²
Area = 22/7 × 7²
Area = 154 cm²
So, the area of the circle is 154 cm².
Looking Around
Find the circumference of a circle that has a radius of 20 cm.
Answer
Is known:
- r = 20 cm
- π = 3,14
Asked:
- Circumference?
Answer:
Perimeter = 2 × × r
Perimeter = 2 × 3.14 × 20
Perimeter = 125.6 cm
So, the circumference of the circle is 125.6 cm.
Finding Diameter
A circle has a circumference of 66 cm. Determine what the diameter of the circle is!
Answer
Is known:
- Perimeter = 66 cm
Asked:
- Circle diameter?
Answer:
Perimeter = × d
In finding the diameter, we will use the formula to find the diameter, namely:
The formula for finding the diameter is d = perimeter /
- d = 66 / (22/7)
- d = (66 × 7) / 22
- d = 21 cm
So, the diameter of the circle is 21 cm.
Thus a brief review this time that we can convey. Hopefully the above review can be used as your study material.
