One Variable Linear Inequality

One Variable Linear Inequality- One variable linear inequality is an open sentence that has only one variable and has degree one and contains a relationship ( > or < ).

For example, look at some sentences like the one below:

1. X > 9
2. 3x – 3 < 8
3. 3b > b + 6
4. 5n – 3 < 3n + 2

Some of the open sentences above use hyphens such as , > or <. Which indicates the sentence is an inequality.

Each of these inequalities only has one variable, namely x, a and n. This inequality is called a one-variable inequality. The variable (variable) of the above inequality to the power of one or also referred to as degree one is called a linear inequality.

One variable linear inequality is an open sentence that has only one variable and degree of one and there is a relationship (, or £ ).

The general form of PtLSV in a variable can be expressed as below:

ax + b < 0, ax + b > 0, or ax + b > 0, or ax + b < 0,with a < 0, a and b are real numbers.

Below are some examples of PtLSV using the x variable, including:

1. 3x – 2 < 0
2. 3x – 2 < 0
3. 5x – 1 > 8
4. 3x + 1 > 2x – 4
5. 10 < 2(x + 1)

Properties of One Variable Linear Inequality

Similar to that in a one-variable linear equation, finding a solution to a one-variable linear inequality can be done by using substitution.

However, you can also do this by subtracting, adding, multiplying, or dividing both sides of the inequality by the same number.

Inequality in mathematics is a sentence or mathematical statement that shows a comparison of the sizes of two or more objects.

As in A < B linear inequality one variable x and C is a non-zero constant.

The inequality A < B is equivalent to:

1. A + C < B + C
2. A – C < B – C
3. A x C < B x C, if C > 0 for all x
4. A x C > B x C, if C < 0 for all x
5. A/C < B/C, if C > 0 for all x
6. A/C > B/C, if C < 0 for all x

You need to note, some of the properties above also apply to the symbol ">" or "<”.

Examples of PtLSV Questions and How to Solve them

Below we will give an example of a problem as well as how to solve it and also the answer to a one-variable linear inequality problem. Here's the full review.

1. One Variable Linear Inequality Addition and Subtraction (PtLSV)

Please note the inequalities below:

x + 3 < 8, where x is a variable from an integer.

For:

x = 1, so 1 + 3 < 8, is true
x = 2, so 2 + 3 < 8, is true
x = 3, so 3 + 3 < 8, is true
x = 4, so 4 + 3 < 8, is false

Substituting x for 1,2, and 3 so that the inequality x + 3 < 8 is true is called a solution to the inequality.

2. Multiplication or division of One Variable Linear Inequality (PtLSV)

Take a look at the following inequalities:

For natural x numbers less than 10, the solution is x = 7, x = 8, or x = 9

Based on the description above, we can conclude that:

 "Every inequality remains equivalent, with the sign of the inequality unchanged, even though both sides are multiplied by the same positive number"

Problems example:

Now consider the following inequalities:

a. –x > – 5, where x is a natural number less than 8. The substitute for x that satisfies is x = 1, x = 2, x = 3 or x = 4.

Another way to solve the inequality problem above is to multiply both sides by the same negative number.

* –x > –5

–1(–x) > – 1(–5), (both sides are multiplied by –1 and the inequality sign remains)

x > 5

The solution is with x = 6 or x = 7.

* –x > –5

–1(–x) < –1(–5), (both sides are multiplied by –1 and the inequality sign changes from > to

x < 5

The solution is x = 1, x = 2, x = 3, or x = 4.

Based on this solution, it turns out that the inequalities that have the same solution are:

–x > –5 and –1(–x) < –1(–5)

so, –x > –5 <=> –1(–x) < –1(–5)

b. –4x <–8, where x is a natural number less than 4. A suitable substitute for x is x = 2, or x = 3. So, the solution is x = 2 or x = 3.

Based on the explanation above, we can conclude that:

"An inequality when both sides are multiplied by the same negative number then the sign of the inequality changes"

Example:

3. About the story 

Question 1.

The sum of two numbers is not more than 120. If the second number is 10 more than the first number, then determine the limit value for the first number.

Answer:

From the problem above, we can see that there are two unknown quantities. That is the first number and also the second number.

So next we will make these two quantities as a variable.

As an example:

We call the first number x, while 

We call the second number y.

From this problem, we also know that the second number is "10 more than the first number", so the following relationship will apply:

y = x + 10

In the problem it is also known that the sum of the two numbers is "no more" than 120.

The sentence "no more" is an indication that the inequality is less than equal (≤). So, the form of inequality that fits the problem is that the inequality is less than equal to.

Then we construct the inequalities like so:

⇒ x + y ≤ 120

Because y = x + 10, so the inequality becomes:

⇒ x + x + 10 ≤ 120

⇒ 2x + 10 ≤ 120

⇒ 2x + 10 – 10 ≤ 120 – 10

⇒ 2x ≤ 110

⇒ x ≤ 55

so that, the limit value for the first number is not more than 55.

Story question 2.

A model of a beam frame made of wire with a length (x + 5) cm, width (x – 2) cm, and height x cm.

• Determine the mathematical model of the required wire length equation in x.
• If the length of the wire used is not more than 132 cm, then determine the size of the maximum value of the beam.

Answer:

So that it is easier for us to understand the problem above, then consider the illustration of the block below:

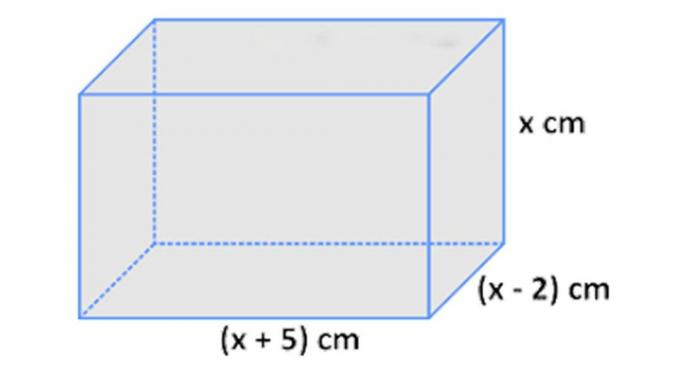
• Determine the mathematical model of the problem above.

For example, K represents the total length of wire needed to make the frame of the beam, then the total length of wire required is the sum of all the edges.

So, the length of K is as follows.

K = 4p(length) + 4l(width) + 4t(height)

K = 4(x + 5) + 4(x – 2) + 4x

K = 4x + 20 + 4x – 8 + 4x

K = 12x + 12

So, we get the mathematical model of story problem number two for the total length of the wire, which is K = 12x + 12.

• Determine the maximum size of the block from the problem above.

The length of the wire must not exceed the length of 132 cm, so we can write the inequality model as follows:

K ≤ 132

12x + 12 ≤ 132

Then we solve the linear inequality of one variable by using a solution like the following:

12x + 12 ≤ 132

⇒ 12x ≤ 132 – 12

⇒ 12x ≤ 120

⇒ x ≤ 10

From the solution x ≤ 10, then the maximum value of x is 10. Thus, the size of the beam for the length, width and height is as follows:

Length = x + 5 ⇔ 10 + 5 = 15 cm

Width = x – 2 ⇔ 10 – 2 = 8 cm

Height = x ⇔ 10 cm

So we get the maximum for the block is (15 × 8 × 10) cm.

Story questions 3.

The sum of two numbers is less than 80. The second number is three times the first number.

Determine the boundaries of the two numbers.

Answer:

Suppose we call the first number as x, then the second number is equal to 3x.

The sum of these two numbers is less than 80. Therefore, the mathematical model is as follows:

x + 3x < 80 ⇔ 4x < 80

The solution of this mathematical model is 4x < 80 ⇔ x < 20.

Therefore, the limit of the first number is not more than 20, while the second number is not more than 60.

Story questions 4.

The surface of a rectangular table has a length of 16 x cm and a width of 10 x cm.

If the area is not less than 40 dm2, then determine the minimum size of the table surface.

Answer:

The length of the table surface is:

• (p) = 16x
• width (l) = 10 x
• area = L.

The mathematical model of the area of ​​the rectangle is as follows:

L = p × l

L = 16x × 10x

L = 160x2

From the problem it is stated that the area is not less than 40 dm2 = 4,000 cm2 so we can write the inequality as follows:

L = 160x2≥ 4.000

160x2≥ 4.000

Then we solve the inequality, with the following solution:

160x2≥ 4.000

⇒ x2≥ 25

⇒ x ≥ ±5

Because size cannot be negative, then the minimum value for x = 5 cm, so we get:

p = 16x cm = 16(5) cm = 80 cm

l = 10x cm = 10(5) cm = 50 cm

Thus, the minimum size of the table surface is (80 × 50) cm.

Story questions 5.

A bicycle is traveling on a road with the equation s(t) = t2– 10t + 39.

If x is in meters and t is in seconds, determine the time interval for the bicycle to have traveled at least 15 meters.

Answer:

The bicycle can cover a distance of at least 15 meters, which means s (t) ≥ 15.

So, the mathematical model is t2– 10t+39 ≥ 15. We can solve this model in the following way:

t2– 10t+39 ≥ 15

⇒ t2– 10t+39 – 15 ≥ 0

⇒ t2– 10t+24 ≥ 0

⇒ (t – 6)(t – 4) ≥ 0

⇒ t ≤ 4 or t ≥ 6

Thus, the time interval for the bicycle to have covered a distance of at least 15 meters is t ≤ 4 seconds or t ≥ 6 seconds.

Story questions 6.

Mr. Irvan has a box car carrying goods with a carrying capacity of no more than 500 kg.

Pak Irvan's weight is 60 kg and he will carry boxes of goods which each box weighs 20 kg. Then:

• Determine the maximum number of boxes that can be transported by Mr. Irvan in one transport!
• If Mr. Irvan is going to transport 115 cities, at least how many times will the boxes be able to be transported all?

Answer:

From the problem we get several mathematical models as follows:

1. For example, x represents the number of cities that a car can transport one way.
2. Each box weighs 20 kg, so x boxes weigh 20x kg.
3. The total weight one way is the weight of the box plus the weight of Mr. Irvan which is 20x + 60.
4. The car's carrying capacity is not more than, then we use the sign "≤”.
5. The carrying capacity is not more than 500 kg so from the provision (3) we get the following inequality model =
   20x + 60 ≤ 500

• Specifies the maximum number of boxes that can be transported in one go.

Determining the number of squares is the same as determining the value of x, namely by solving the inequalities below:

20x + 60 ≤ 500

⇒ 20x ≤ 500 – 60

⇒ 20x ≤ 440

⇒ x ≤ 22

From this solution, we get the maximum value of x which is 22. Thus, each time the box car can carry a maximum of 22 boxes.