Introduction to Variables: Variables, Coefficients, Constants, Terms, Sample Problems

In seventh grade (7) in mathematics we will learn about variable recognition.

The introduction of these variables includes variables, coefficients, constants, and terms. For more information, see the full review of the following Variable Recognition.

Algebra

Linguistically, algebra means uniting various separate parts. In this case, the part in question includes the constituent elements of an algebraic number. Such as: variables, coefficients, constants, terms, factors, like terms, dissimilar terms.

To better understand algebra, the following is an explanation for each of the constituent elements of algebra.

1. Variable

Variable is a substitute symbol for a number whose value is not clearly known.

Variables are also known as variableIn general, these variables are denoted by lowercase letters such as a, b, c, … z.

2. Coefficient

Coefficient is a number that contains a variable of a term in algebraic form.

3. Constant

The term of an algebraic form that is in the form of numbers and does not contain variables is called constant.

4. Tribe

Tribe is a variable as well as its coefficient or constant in algebraic form separated by the operation of sum or difference.

In the previous review, we studied the multiplication of an integer, that is, the repeated addition of the integer.

As an example:

3 x 4 = 4 + 4 + 4
4 x 5 = 5 + 5 + 5
6₃ = 6 x 6 x 6

If we describe the multiplication form above in algebraic form, we will get various forms as below:

3 x a = a + a + a = 3a
4 x x = x + x + x + x = 4x
4 x p = p + p + p + p = 4p
y3 = y x y x y

The form of 3a, 4x, y3, 5×2 + 4, etc. is called algebraic form. An algebraic form containing letters and numbers. The letter is referred to as variable. Numbers in algebraic form that contain variables, are called coefficient, while a number that does not contain a variable is referred to as constant.

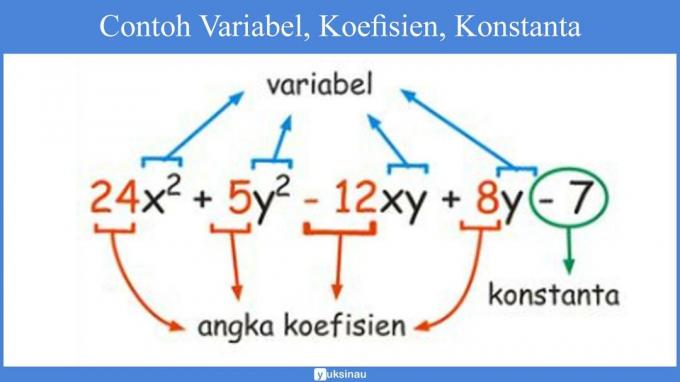
Example:

1. In the algebraic form 3a, 3 is called as coefficient a and a are called as variable.
2. In the algebraic form 2n + 5, 2 is called coefficient n, n is called variable, and 5 is called constant.

In integers, if we write a = b x c, then b and c are called factors of a. Meanwhile, in algebraic form, if we write 3 (x + 2), then 3 and (x + 2) are called multiplication factors.

Tribe Example

Consider the following algebraic form.

5x² + 2x + 7y – 3y + 10

The algebraic form above consists of 5 terms, including: 5x², 2x, 7y, –3y, and 10. This form has one similar term, namely 7y and –3y.

In algebraic form, like terms differ only in their coefficients.

Examples of Algebraic Forms

Problem 1.

Write the simple form of the numbers below:

2x²– 3x – 9 / 4x² – 9 ?

Answer:

The factoring of the numerator is:

2x² – 3x – 9 = 2x² – 6x + 3x – 9

= 2x ( x – 3 ) + 3 ( x -3)

= ( 2x + 3 ) ( x – 3 )

The factoring of the denominator is:

4x² – 9 = ( 2x – 3 ) ( 2x + 3 )

So we will get:

2x² – 3x – 9 / 4x² – 9 = ( 2x + 3 ) ( x – 3 ) / ( 2x – 3 ) ( 2x +3 )

Then remove the factor that has the same value between the numerator and denominator, which is 2x + 3. Then we will get the final result as follows:

2x² – 3x – 9 / 4x² – 9 = x -3 / 2x – 3

So, the result of the simple form of the number

2x²– 3x – 9 / 4x² – 9 is x -3/2x – 3.

Question 2.

What is the result of the following algebraic number: 2 ( 4x – 5 ) 5x + 7 ?

Answer:

2 ( 4x 5 ) 5x + 7 = 8x -10 – 5x + 7

= 8x – 5x – 10 + 7

= 3x – 3

So, the result of the number

2 ( 4x – 5 ) 5x + 7 is 3x – 3.

Problem 3.

What is the result of the following algebraic number ( 2x – 2 ) ( x + 5 ) ?

Answer:

( 2x – 2 ) ( x + 5 ) = 2x ( x + 5 ) – 2 ( x + 5 )

= 2x ² + 10x – 2x – 10

= 2x ² + 8x – 10

So, the result of the number ( 2x – 2 ) ( x + 5 ) is

2x ² + 8x – 10.

Problem 4.

What is the result of the following algebraic number: 2 / 3x + 3x + 2 / 9x ?

Answer:

2/3x + 3x + 2/9x = 2. 9x + ( 3x + 2 ). 3x

= 18x + 9x² + 6x / 3x. 9x

= 9x² + 24x / 3x. 9x

= 3x ( 3x + 8 ) / 3x. 9x

Then we remove the common factor between the numerator and denominator. So we will get the result as:

2/3x + 3x + 2/9x = 3x + 8/9x

So, the product of 2/3x + 3x + 2/9x isx

3x + 8 / 9x.

Question 5.

Write the simple form of the following algebraic number: 3x² – 13x – 10 / 9x² – 4 ?

Answer:

The factoring of the numerator is:

3x² – 13x – 10 = 3x² – 15x + 2x – 10

= 3x ( x – 5 ) + 2 ( x – 5 )

= ( 3x + 2 ) ( x – 5 )

The factoring of the denominator is:

9x² – 4 = ( 3x + 2 ) ( 3x – 2 )

So we will get:

3x² – 13x – 10 / 9x² – 4 = ( 3x + 2 ) ( x – 5 ) / ( 3x + 2 ) ( 3x – 2 )

Then we remove the common factor between the numerator and denominator, which is 3x + 2. So we will get the result as:

3x² – 13x – 10 / 9x² – 4 = x – 5 / 3x – 2

So, the result of the simple form of the number 3x² – 13x – 10 / 9x² – 4 is

x – 5 / 3x – 2.

Question 6.

What is the result of the following algebraic number ( 2x – 2 ) ( x + 5 ) ?

Answer:

( 2x – 2 ) ( x + 5 ) = 2x ( x + 5 ) – 2 ( x + 5 )

= 2x² + 10x – 2x – 10

= 2x² + 8x – 10

So, the result of the number ( 2x – 2 ) ( x + 5 ) is

2x² + 8x – 10.

Question 7.

Subtract the following numbers: 9a – 3 from 13a + 7 ?

Answer:

( 13a + 7 ) – ( ​​9a – 3 ) = 13a + 7 – 9a + 3

= 13a – 9a + 7 + 3

= 4a + 10

So, the result of subtracting the numbers 9a – 3 from 13a + 7 is

4a + 10.

Question 8.

What is the result of the following algebraic number: ( 2x – 4 ) ( 3x + 5 ) ?

Answer:

( 2x – 4 ) ( 3x + 5 ) = 2x ( 3x + 5 ) – 4 ( 3x + 5 )

= 6x² + 10x – 12x – 20

= 6x² – 2x – 20

So, the result of the number ( 2x – 4 ) ( 3x + 5 ) is

6x² – 2x – 20.

Problem 9.

What is the result of factoring the number 4x .?² – 9y² ?

Answer:

You have to remember that the form factor is algebraic like so:

a² – b² = ( a + b ) ( a – b )

4x² = ( 2x )²

9y² = ( 3y )²

So the factor of the number 4x² – 9y² is

4x² – 9y² = ( 2x + 3y ) ( 2x – 3y )

So, the result of factoring the number 4x² – 9y² is

( 2x + 3y ) ( 2x – 3y ).

Question 10.

What is the result of the following algebraic numbers: ( 2a – b ) ( 2a + b ) ?

Answer:

( 2ab ) ( 2a + b ) = 2a ( 2a + b ) – b ( 2a + b )

= 4a² + 2ab – 2ab – b²

= 4a² – b²

So, the result of the number ( 2a – b ) ( 2a + b ) is

4a² – b².

Question 11.

What is the result of factoring the following algebraic number: 16x² 9y² ?

Answer:

You have to remember that the form factor is algebraic like so:

a² – b² = ( a + b ) ( a – b )
16x² = ( 4x )²
9y² = ( 3y )²

So the factor of the number 4x² – 9y² is:

16x² – 9y² = ( 4x + 3y ) ( 4x – 3y )

Therefore, the result of factoring the number 16x² 9y² is

( 4x + 3y ) ( 4x – 3y ).

Thus a brief review of Variable Recognition that we can convey. Hopefully the above review regarding Variable Recognition can be used as your study material.