Cube: Elements, Properties, Volume and Surface Area Formulas

Cube: Elements, Properties, Volume and Surface Area Formulas and Example Problems – How to calculate the volume and surface area of ​​a cube?, On this occasion About Knowledge.co.id will discuss it and of course about other things that also surround it. Let's take a look at the discussion in the article below to better understand it.

---

Cube: Elements, Properties, Volume and Surface Area Formulas and Example Problems

---

Build a cube is a building space that has a three-dimensional shape that has been limited by six sides and the sides are congruent or square.

Then Build the Cube Space can also be called a regular six-plane that is shaped similar to a rectangular prism.

---

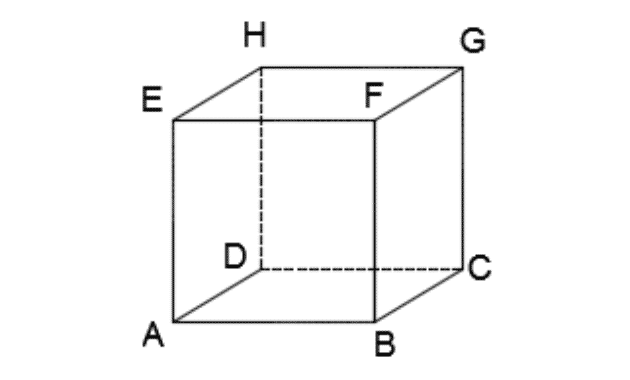
Cube Elements

We can see with the picture of the cube above, pay close attention because we get an element from the cube above, which is below:

• Side or plane

The definition of the side of the cube is the area that limits the cube. If we look at the picture of the cube above, we can conclude that the cube is a shape that has 6 sides, all of which are square.

And the sides are:

• • Down side ( ABCD )
  • Upside ( EFGH )
  • Front side ( ABFE )
  • Back side ( DCGH )
  • Left side (BCGF)
  • Right side (ADHE)

• ---

  Lateral

The ribs on the cube mean the intersection line between the 2 sides of the cube and looks like the skeleton that makes up the cube.

Then the edges of the cube image above are AB, BC, CD, DA, AE, BF, CG, DH, EF, FG, GH, and HE.

• Corner point

The vertex is the point of intersection between 2 or 3 edges. In the picture of the cube above we can get the angle, which has 8 angles, namely A, B, C, D, E, F, G, and H.

• The plane diagonal or the side diagonal

If we give a long line in each of its opposite corners on each side then we will see the shape of an isosceles triangle, now that line is called the diagonal of the field or side.

In the example of the cube image above, we can find 12 diagonal planes or 12 sides, namely AF, BE, BG, FC, CH, DG, AH, DE, BD, AC, EG, and HG.

• space diagonal

In the example of the cube image above, we can get 4 diagonals of space, namely the lines BH, DF, AG, and EC.

• Diagonal plane

The definition of the diagonal plane itself is a plane formed from 2 diagonal lines and 2 parallel cube edges.

In the example of the cube image above, we can get 4 diagonal planes, namely ACGE, DBFH, ABGH, EFCG.

---

Cube Properties

Next we discuss the properties of the cube, which consists of:

In the picture of the cube above, we can see that the cube consists of: ABCD.EFGH in each corner where the shape has the following properties:

• All Sides Of A Square Cube:

If you pay attention, on the sides ABCD, EFGH, ABFE, DCGH, BCGF and so on have a square shape and have the same area.

• All edges of a cube have the same length:

The edges of the cube, namely: AB, BC, CD, DA, EF, FG, GH, HE and so on, have the same length.

• Each diagonal of a cube has the same length:

Consider the line segments BG and CF in the cube ABCD.EFGH. The two lines are a diagonal of the cube ABCD.EFGH in the BCGF plane which has the same length.

• Each diagonal space in the cube has the same length:

From the picture of the cube ABCD.EFGH above, there are 4 space diagonals, namely HB, DF, AG and CE, all of which are the same length.

5. Each Diagonal Area in the Cube Has a Rectangular Shape:

Consider the ACGE diagonal plane in the cube ABCD.EFGH figure above. It is clear that the diagonal area has a rectangular shape.

---

Cube Volume Formula

Now, after explaining the meaning of the cube and what elements are in the cube space. Now we will explain about the formula for the area and volume of the cube itself, which is as follows:

V = S³

Information :

• • V = volume of the cube ( cm³ )
  • S = side length of cube (cm)

The formula for the area of ​​the cube itself is as follows:

---

Area formula for cube Rumus

L = 6.s²

Information :

• • L = surface area of ​​the cube (cm)
  • S = side length of cube (cm)

---

Cube Surface Formula

• Cube Surface Area:
  • L = 6 x edge x edge = 6 x s²
• Perimeter of the Cube Surface:
  • K = 12 x edge = 12 x s

---

Examples of Cube Problems

---

Problem 1:

Answer and discuss:

Volume of Cube = V = s³

So Vol = 30 x 30 x 30

Volume = 27000 m³

Perimeter of a Cube = K = 12 x s

K = 12 x 30

= 360 cm

The formula for the surface area of ​​a cube = L = 6 x s²

L = 6 x 30 x 30

L 5400 cm²

Problem 2:

Budi's wardrobe is in the form of a cube that has the same length, width, and side which is 4 meters. Calculate the volume of Budi's wardrobe?

Answer and discussion:

If it has been stated that they have the same length, width, and side, then it is unmistakable that they are one of the properties of the cube, therefore it can be directly calculated the volume of the cupboard as following:

Wardrobe volume: 4³ = 4 x 4 x 4 = 64 m³

Problem 3

There is a surface of a cube whose side length = 10 cm. Find and calculate the surface area of ​​the cube!

Solution:

Given: s = 10 cm

asked: L = …?

Answer:

L = 6 x s²

L = 6 x 10 x 10

L = 600 cm²

So, the surface area of ​​the cube is = 600 cm²

Question 4

It is known that the volume of a cube is 1331 cm³ but the length of the edge of the cube does not exist, then you have to find how long the side of the cube is?

Answer:

It is known that = v = 1331 cm³

The question = length of the side of the cube?

Volume = s³

1331 cm³ = s³

1331 = 11

S = 11 cm

So, the side length of the cube is 11 cm.

That's the review from About Knowledge.co.id about Cube: Elements, Properties, Volume and Surface Area Formulas and Example Problems, Hopefully it can add to your insight and knowledge. Thank you for visiting and don't forget to read other articles.