Logarithmic Equations: Formulas, Properties, Example Problems and Discussion Pembahasan

Logarithmic Equations: Formulas, Properties, Example Problems and Discussion – What is a Logarithmic Equation and an example of a problem? On this occasion, Seputardunia.co.id will discuss it and of course about other things that also cover it. Let's take a look at the discussion in the article below to better understand it.

---

Logarithmic Equations: Formulas, Properties, Example Problems and Discussion Pembahasan

---

A logarithm is a mathematical operation that is the inverse (or inverse) of the exponent or power. In this formula, a is the basis or principal of the logarithm. Judging from the origin of the words, the word Algorithm has a rather strange history. People only find the word Algorism which means the process of calculating with Arabic numerals.

Logarithmic equationa is an equation whose variable is a numerus or logarithmic base number. Logarithms can also be interpreted as mathematical operations that are the inverse (or inverse) of the exponent or power.

A person is said to be an "Algorist" if he counts using Arabic numerals. Linguists tried to find the origin of this word but the results were less than satisfactory. Finally, historians of mathematics found the origin of the word which comes from the name of the author of the book The famous Arabic, namely Abu Abdullah Muhammad Ibn Musa Al-Khuwarrismi is read by westerners as Algorism.

The inventor was a mathematician from Uzbekistan named Abu Abdullah Muhammad Ibn Musa Al-Khwarizmi. In western literature, he is better known as Algorism. This call is then used to refer to the concept of the algorithm he found.

Abu Abdullah Muhammad Ibn Musa Al-Khuwarizmi (770-840) was born in Khwarizm (Kheva), a city south of the Oxus river (now Uzbekistan) in 770 AD. His parents then moved to a place south of Baghdad (Iraq), when he was a child.

A work using Indian numerals, which was first translated and used in the West is entitled al-jam' wa'l-tafriq bi hisab al-hind (Addition and Subtraction in Indian Arithmetics). The book is the glorious work of the Muslim mathematician Muhammad ibn Musa Al-Khwarismi (780-850M).

John Napier was an English mathematician, born at Merchiston Castle Eidenburg. Napier finished school in France at the age of 13, then he went on to the University of St. Andrews in Scotland.

In 1612 AD, he discovered a system which he named "logarithm" which was derived from the name khwarizmi. Now his findings, better known as the Napier logarithm (Napierian Logarithms).

Napier once made a table carved in ivory that looked like bone. Then, they named it Napier's Bones.

When Napier's book on logarithms was published in 1614, it amazed scientists as much as the invention of the modern-day calculator.

With the help of logarithms they can do difficult multiplication and division in a fast and easy way for the first time. Napier spent his life fiddling with mathematics.

He died in 1617 at the age of 67 and was buried in Edinburgh. (Johanes, et al: 33).

Because seeing the base numbers used in logarithms at that time was not pleasant, Henry Briggs (British mathematician) created The Table of Common Logarithms with base 10 numbers immediately After that.

---

Logarithmic Formula

a^c = b → log b = c

Information:

a = base
b = dilogarithmic number
c = result of logarithm

---

Logarithmic Properties

loga = 1

log 1 = 0

log aⁿ = n

log bⁿ = n • log b

log b • c = log b + log c

log b/c = log b – log c

log b m = m/n • log b

log b = 1 b log a

log b • b logs c • c log d = log d

log b = c log b c log a

---

Properties of Logarithmic Equations

• ---

  Logarithmic Properties of Multiplication:

A logarithm is the result of the sum of two other logarithms where the value of the two numerals is a factor of the initial numeric value.

^alogs p. q = ^alog p + ^alog q

With the condition that = a > 0, a \ne 1, p > 0, q > 0.

• ---

  Logarithmic Multiplication:

A logarithm a can be multiplied by a logarithm b if the numeric value of logarithm a is equal to the base number of logarithm b. The result of the multiplication is the new logarithm with the base number equal to logarithm a, and the numerus value equal to logarithm b.

^alog b x ^blogc = ^alog c

With the condition that = a > 0, a \ne 1.

• ---

  Logarithmic Properties of Division:

A logarithm is the result of subtracting from two other logarithms the value of the two numerals is a fraction or division of the numeric value of the initial logarithm.

The conditions are = a > 0, a \ne 1, p > 0, q > 0.

• ---

  Inversely proportional logarithm properties:

A logarithm is inversely proportional to another logarithm whose base number and numeric values ​​are interchangeable.

^alogb = 1/^blog a

With the condition that = a > 0, a \ne 1.

• ---

  Logarithmic Opposite Sign:

A logarithm is opposite in sign to a logarithm whose numerus is an inverse fraction of the numeric value of the initial logarithm.

^alog p/q = – ^alog p/q

The conditions are = a > 0, a \ne 1, p > 0, q > 0.

• ---

  Logarithmic Properties of Powers:

A logarithm with its numeric value is an exponent (power) and can be used as a new logarithm by removing the exponent as a multiplier.

^alog b^p = p. ^alog b

With the condition that = a > 0, a \ne 1, b > 0

• ---

  Power of Logarithmic Principal Numbers:

A logarithm, i.e. the base number is an exponent (power) which can be used as a new logarithm by removing the exponent into a divisor.

a^plogb = 1/p^alog b

With the condition that = a > 0, a \ne 1.

• ---

  Logarithmic Fundamental Numbers Comparable to Numeric Powers:

A logarithm that is where the numerus value is an exponent (power) of the value of the base number which has the same result as the value of the power of the numerus.

^alog a^p = p

• ---

  Logarithmic powers:

A number that has a power in the form of a logarithm, the result of the exponent is the value whose numerus is the logarithm.

a ^alog m = m

The conditions are = a > 0, a \ne 1, m > 0.

• ---

  Changing the Base Logarithm:

A logarithm can also be broken down into a ratio of two logarithms.

^plog q = ^alog p/^a log q

With the condition that = a > 0, a \ne 1, p > 0, q > 0

---

Logarithmic Example

Logarithms also have their own examples of numbers, which are as follows:

---

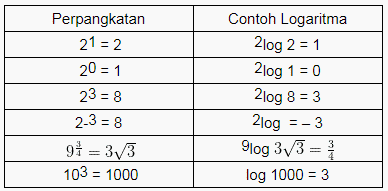
Example of Logarithmic Equation Problems

---

Problem 1

Known logarithm ³log 5 = x and ³log 7 = y. then, the value of ³log 245 1/2 is….

Solution:

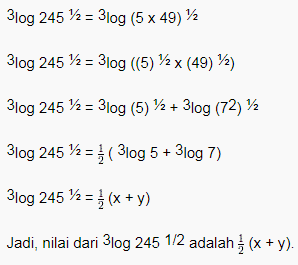
Problem 2

1. Value of ²logs 4 + ²logs 12 – ²logs 6 =…

---

1. 8
2. 6
3. 5
4. 4
5. 3

---

Discussion:

For problems like the one above, we need to remember the logarithmic property

^alog(b.c) = ^alog b + ^alog c, and

^alog  = ^alog b – ^alog c

so, to solve the problem above, we use both properties of the logarithm. Where the calculation will be:

²logs 4 + ²logs 12 – ²log 6 = ²log

= ²log 8

Then, for the final solution, we need to remember the next property, namely:

^alog  = n. ^alog b

→ 8 =

So, the final solution will be like this:

²log 8 = ²log

= 3. ²log 2 → don't forget this one: ^aloga = 1

= 3. 1

= 3 ( E )

---

Problem 3

If log 3 = 0.4771 and log 2 = 0.3010, then the value of log 75 =…

---

1. 0,7781
2. 0,9209
3. 1,0791
4. 1,2552
5. 1,8751

---

Discussion:

For questions with this model, there is a key to the process that we must understand. That is a description that shows the value of log 2 and log 3. With this additional information, it means that what should be on our mind is how to change the form of log 75 into a logarithmic form that contains elements of numbers 2 and 3.

---

→ 75 = 3. 25 = 3 .

So, if we change the number 75 by 3, we will get:

---

log75 = log( 3. ) → with this, we have to remember the properties: ^alog(b.c) = ^alog b + ^alog c

= log 3 + log → don't forget that: ^alog  = n. ^alog b

= logs 3 + 2. log 5

---

The point is to change the number 5 in the log 5, because in the questions that are given information are log 2 and log 3, while log 5 is not given any information.

---

For that, the trick that needs to be done here is:

→ 5 =

---

We need to convert the number 5 into a number that is contains the element number 2 and its value does not change (still value 5). So, if we solve it, it will be:

---

log 75 = log 3 + 2. log → of course still remember the nature ^alog  = ^alog b – ^alogc, right?

= log 3 + 2 ( log 10 – log 2 ) → log 10 = ¹⁰log 10 = 1 → ^aloga = 1

= 0,4771 + 2 ( 1 – 0,3010 )

= 1.8751 ( E )

---

Question 4

Is known ²log 3 = 1.6 and ²log 5 = 2,3; value of ²logs..

---

1. 10,1
2. 6,9
3. 5,4
4. 3,2
5. 3,7

---

Discussion:

Slightly similar to the previous question, by knowing any information in the question regarding value of a logarithm of a number, then what we need to do is to convert it into a form containing a number element that matches the information.

---

→ 125 = 5. 5. 5 =

→ 9 =

---

So, if we solve the problem, it will be:

²log = ²log → predictable right? Here we need character: ^alog  = ^alog b – ^alog c

= ²logs – ²log

---

Then, the logarithmic property that we use next is the property:

^alog  = n. ^alog b

---

So, the above equation will be:

= 3. ²logs 5 – 2. ²log 3

= 3. ( 2,3 ) – 2. ( 1,6 )

= 6,9 – 3,2

= 3.7 ( E )

---

That's the review from Seputardunia.co.id about Logarithmic Equations: Formulas, Properties, Example Problems and Discussion Pembahasan ,Hopefully it can add to your insight and knowledge. Thank you for visiting and don't forget to read other articles