Mathematical Probability Formulas and Examples of Probability Problems

Formula. Co. ID - will discuss the meaning, types, kinds, formulas, and examples of mathematical probability problems in detail and complete. Opportunity in mathematics itself is a way to find out the probability of an event, for more details, please refer to the explanation below:

Understanding Opportunity

Opportunity can be interpreted as a way to find out the possibility of an event happening. in a problem there must be uncertainty caused by an action that sometimes results in another.

For example, if a coin is tossed up, the result can be a side the image (G) or the number side (A), then the side that will appear cannot be said with certainty the truth.

As a result of the event of throwing a coin, there are one of two possible events, namely the appearance of side G or A. The activity of throwing a coin can be said as a random action. The action can be repeated up to several times and the series of actions is called an experiment.

Relative Frequency

Frequency is the ratio between the number of experiments performed and the number of outcomes observed. And from the experiment of throwing the coin, the relative frequency can be formulated as follows:

Sample Room 

The sample space is the set of all possible experimental events (outcomes). The sample space is denoted by S.
Example
a. The sample space for rolling a die is S =(1,2,3,4,5,6)
b. The sample space on the tossing of a coin is S= (A, G)

Determining the Sample Space

The sample space of the result of throwing two currencies can also be determined using a table (list) as follows.

The sample space is S = {(A, A), (A, G), (G, A), (G, G)}
Event A1 which can contain two images = (G, G)
Event A2 which cannot load image = (A, A)

Sample Point

Sample points are members of the sample space

Example
The sample space of S is = ((A, A), (A, G), (G, A), (G, G))
The sample points are = ((A, A), (A, G), (G, A), (G, G))

Mathematical Probability Formula

From the results of the experiment tossing a coin the result is G or A. If the experiment is tossed 10 times and G appears 4 times, then the relative frequency of G appearing is 4/10. And if the experiment is carried out 10 more times and G appears 3 times so that in 20 times G appears 7 times, then the relative frequency that appears for G in 20 trials is 7/20.

1. Probability of Event A or P(A)

The probability of this event can be determined in the following way.
S = {1,2,3,4,5,6} then the value of n(S) = 6
A = {2,3,5} then the value of n(A) = 3

Thus, the probability of an event A whose number of members can be expressed in n (A) can be expressed by the following formula.

Opportunity Value

Opportunity values ​​that can be obtained range from 0 to 1. For each event A, the limits of the value of P(A) can be mathematically written as follows.

0 P(A) 1 where P(A) is the probability of an event A

If the value of P(A) = 0, then event A is an impossible event, then the probability is 0.
Example:
Sunrise from the south is an impossible event, so the probability is 0.
If P(A) = 1, then the event of A is a definite event

1. Expectation Frequency

Expected frequency is an event that is the expectation of the number of events that appear from a number of experiments that have been carried out. Mathematically it can be written as follows

Expected frequency = P(a) x number of trials

Example:
In the experiment of tossing a dice that has been carried out 60 times, then:
Probability of getting 2 points = 1/6
Expected frequency of eye 2 = P (eye 2) x number of trials
= 1/6 x 60
= 10 times

2. Compound Occurrence

A compound event is two or more events that are operated so that a new event is formed.

An event K and a complement event in the form of K' satisfy the equation:

P(K) + P(K') = 1 or P(K') = 1 – P(K)

Sum of Opportunities

1. Mutual Events

Two events A and B can be said to be mutually exclusive if none of the elements occur in event A which is the same as the element that occurs in event B, then the probability that either A or B may occur, the formula is is:

P(A u B) = P(A) + P(B)

2. Events Don't Get Rid of Each Other

The meaning is that there is an element A that is equal to element B, the formula can be written as follows:

P(A u B) = P(A) + P(B) – P(A n B)

3. Conditional Event

A conditional event can occur if event A can affect the occurrence of event B or vice versa. Therefore it can be written as follows:

P(A n B) = P(A) x P(B/A)

or

P(A n B) = P(B) x P(A/B)

Because the events are mutually influential, the formula can be used:

P(A n B) = P(A) x P(B)

Example of Opportunity Questions

Example Question 1

1. In an experiment tossing a coin 120 times, it turns out that the probability of getting a number is 50 times. Determine the relative frequency of appearance of the number and the relative frequency of appearance of the image!

Solution:

a). The relative frequency of appearing numbers = Many numbers that appear/Many trials
= 50/120
= 5/12

b). Relative frequency of appearing images = Many images appearing/Many trials
= (120 – 50) / 120
= 70/120
= 7/12

Example Question 2

2. Two dice are tossed together. Determine the probability of the following events
a. Probability of rolling the first dice is 4
b. The probability of getting a dice is 9

Solution:

We first create a sample space for the experiment of hitting two dice as follows.

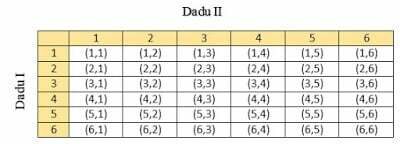
a. The sum of the first dice is 4, meaning the second dice may be 1,2,3,4,5, or 6. Thus, the event that the first dice appears on a 4 is:
M = {(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)}
So, P (dice I edge 4) = n(M)/n(S) = 6/36 = 1/6

b. The event that the sum of the dice is 9 is:
N = {(3,6), (4,5), (5,4), (6,3)}
So, the value of P(sum of 9) = n(N)/n(S) = 4/36 = 1/9

Well, that's the mathematical probability material that can be delivered, hopefully it will be useful ...

Other Formulas:

• Mean, Median, and Mode Data Group Formulas
• Arithmetic Sequence