Formula for the Surface Area of a Quadrangular Pyramid and Example Problems
Surface Area of a Rectangular Pyramid – A quadrilateral pyramid is a geometric shape bounded by a rectangular base and triangular upright sides. The following is a complete explanation of how to calculate the surface area of a quadrilateral pyramid. For more details, see the discussion below

Table of contents :
Rectangular pyramid
To calculate the area of a quadrilateral pyramid, it is necessary to first know the parts that make up a rectangular pyramid, including:
(BCDE) = rectangular base
(BCDE, ABC, ACD, ABE, ADE) is a side plane
(A, B, C, D, E) is the vertex of
(AB, AC, AD, AE, BC, CD, DE, BE) are edges
Volume = 1/3 x Area of base x height
Area of base = s x s
Area = Area of Base + (4 x Area of perpendicular triangle)
Quadrilateral Pyramid Nets
Formula for the Surface Area of a Quadrangular Pyramid
To find the surface of the pyramid can use the equation below.
L = area of base + area of blanket
If the base of the pyramid is square, then the equation becomes
L = ( s x s ) + ( 4 x 1/2 x s x h. blanket)
If the base has a rectangular shape then the equation is
L = ( p x l ) + ( 2 x 1/2 x p x t.blanket ) + ( 2 x 1/2 x l x t.blanket )
Formula Description:
L is the surface area of the pyramid
p is the length of the base of the pyramid
l is the width of the base of the pyramid
t.blanket is the height of the blanket triangle
Look at the picture of the rectangular pyramid below lima
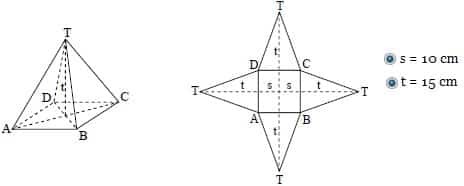
Measure the surface area of a regular rectangular pyramid (with a square base). Pyramid T. ABCD has 5 sides consisting of a base that has a square shape and 4 sides that are isosceles triangles.
The square base ABCD has area = s x s unit area. Each TAB, TBC, TDC, and TAD has the shape of an isosceles triangle. Area TAB = Area TBC = Area TCD = Area TAD = x s x t.
The area of the base is s x s = 10 x 10 = 100 cm²;
The area of the vertical side is 4 x (½ x 10 x 15) = 4 x 5 x 15 = 20 x 15 = 300 cm²
The area of a rectangular pyramid is 100 cm² + 300 cm² = 400 cm².
Problems example
Example Question 1
Take a look at the image below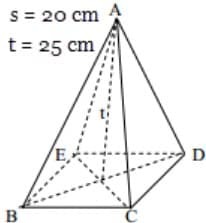
Is known
The side length of the base is 20 cm and the height of the pyramid is 25 cm.
Determine the surface area of the quadrilateral
Answer:
The area of the base is s x s
= 20 x 20 = 400 cm²;
Area of upright side = 4 x (½ x 20 x 25)
= 4 x 10 x 25
= 40 x 25
= 1000 cm²
Area of a rectangular pyramid
= 400 cm² + 1000 cm²
= 1,400 cm²
Example Question 2.
A rectangular pyramid has a length of 20 cm and a width of 15 cm. The height of the blanket triangle is 10 cm.
What is the surface area of the pyramid?
Answer:
Surface Area Formula = ( p x l ) + (2 x 1/2 x p x t.blanket) + (2 x 1/2 x l x t.blanket)
= ( 20 x 15 ) + (2 x 1/2 x 20 x 10) + ( 2 x 1/2 x 15 x 10)
= 300 + 200 +150
L = 650 cm2
So the surface area of the pyramid is 650 cm2
Example Question 3
A pyramid with a square base has a side length of 12 cm. If the height of the pyramid is 30 cm, what is the volume of the rectangular pyramid?
Solution
Is known :
Side length of base = 12 cm
Height of pyramid = 30 cm
Answer
V =. s. s. pyramid height
= x 12 x 12 x 30
= x 4320
= 1440 cm3
So, the volume of the pyramid is 1440 cm3
Example Question 4
If a rectangular pyramid is 10 cm long and 12 cm high. Calculate the surface area of the pyramid!
Is known :
Length = 10 cm
Height = 12 cm
Wanted: Surface area of the pyramid (L)
Answer:
L = Area of base + ( 4 x area of blanket )
To calculate the area of a quadrilateral pyramid, first determine the area of the base and the area of the four sides
Area of Base = 10. 10 = 100 cm2
So, the surface area of the quadrilateral is:
L = area of base + area of four sides
= (10. 10 ) + ( 4 x (½. 10. 13 )
= 100 + 260
= 360 cm2
Thus the discussion about the surface area of a quadrilateral pyramid, Hopefully useful
Other Articles:
- Triangle Surface Area Formula and Volume Formula
- Cone Surface Area Formula and Volume Formula
- The formula for the surface area of the cuboid, the area of the base, the area of the sides
- The formula for the surface area of a cylinder, the area of the base, the area of the blanket, the volume and examples of problems
