Vector Quantity: Definition and Examples of Vector Quantity

Vector quantity – is a quantity that has both value and direction. That is, the value of the quantity is determined by the direction. The following is a complete discussion of vectors and some examples. For more details, see the discussion below

Examples of Vector Quantities

Examples of general vector quantities are velocity, acceleration, force, impulse, momentum, displacement, magnetic field, electric field, and pressure (Pa).

Speed

Velocity is an example of a vector quantity. The reason is that the value of this quantity can be determined in the direction of motion of an object experiencing velocity. In writing, the speed is written in full starting from the value, unit, and direction.

Style

Force is a quantity obtained by multiplying the mass of an object in motion with the acceleration of its motion. Force has units of N or Newton, but can also be written in units of kg.m/s2. A force is an example of a vector because its value is affected in which direction the force is moving.

Pressure

Pressure is a quantity that expresses the force acting on one unit area. Pressure is also an example of a vector quantity. The reason is because pressure can move in any direction, so it is necessary to know which direction the force on the pressure is moving. Pressure is expressed in units of Pascal or Pa

Unit Vector

for a two-dimensional vector, meaning that the vector will form an angle to one of the Cartesian axes (x or y). Another thing that is necessary before starting to draw is because you can use unit vector notation to describe a vector's magnitude and direction.

A unit vector is a vector that has a magnitude of one unit and has a different notation for each Cartesian axis (unit vector i for describing the Cartesian x axis and i for the y axis).

For example, there is a vector a that points 2 units to the right (x-axis) and 3

unit up (y axis), we can make the notasniya a = 2i + 3j.

This can be calculated by squaring the existing numbers, adding them up, then taking the roots. Almost like the formula for finding slashes in Pythagoras

Example

What is the vector size of a equal to 2i + 3j ?
= √ (22) + (32)
= √4 + 6
= √10

How to Draw

For example, suppose there is a vector a that measures 10 m from a point A to point B and points to the positive x-axis. Then how to draw the vector?

First, you have to make an example first. Example: every 5 lengths we make with 1 cm on paper (this is just an example). With that example, then make an arrow (vector) with a length of 2 cm pointing to the right (positive x axis).

So the image becomes:

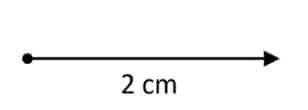
Example of drawing 2

There is a vector B which has a magnitude of 60 m from point P to point Q and forms an angle of 45 degrees with the positive x-axis.

First, make an example. For example, 20 m = 1 cm. That means, you have to make a 3 cm long arrow. And form a 45 degree angle

Then the image becomes

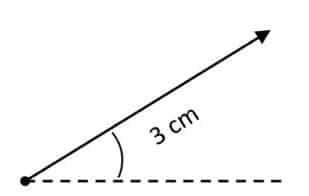
Difference Between Vector and Scalar

From the description and explanation above, it can be concluded that there are several differences between vectors and scalars. These differences include:

1. The value of the vector quantity is determined by the direction, while the value of the scalar quantity is not determined by the direction.
2. Vector quantities are written with complete values, units, and directions, but scalar quantities are written with complete values ​​and units only.

That's the discussion about vectors, hope it's useful

Other Articles:

• Scalar Quantities: Definition, Examples, and Differences between Scalars and Vectors
• Potential Energy: Definition, Formulas, Types, and Examples
• Moment of Inertia Formula with Factors and Example Problems