The formula for the area of a trapezoid along with examples of the problem
Formula.co.id – After previously we discussed about area formula for cone this time we will discuss material about the formula for the area of a trapezoid, we will describe in detail and complete the definition of a trapezoid, properties, formulas, and examples of problems from a trapezoid.
Table of contents :
Definition Trapezoid
What is a Trapezoid? you already know, Trapezoid is a two-dimensional flat shape which is also formed by 4 edges which are parallel but not the same length.
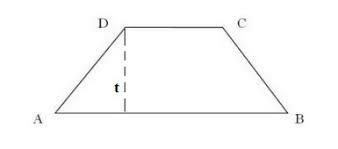
Trapezoidal Properties
Trapezoid also has its own properties, namely:
- A trapezoid has 4 sides and 4 vertices.
- Trapezoid also has a pair of sides that are very parallel but not too long.
- A trapezium has an angle between which the parallel sides are 180o.
Formula Trapezoid
Area of trapezoid =
L = x number of parallel sides x height
Perimeter of trapezium =
K = sum of all sides (eg AB+BC+CD+DA)
Sample Question Area Trapezoid
- If a trapezium has parallel sides that are 4 cm and 10 cm long and 5 cm high, find and calculate the area of the trapezium!
Solution:
Is known :
parallel side = a1 = 4 cm,
b1 = 10 cm
t = 5 cm
asked: L = …?
Answer:
L = x (a1 + a2) x t
L = x (4 cm + 10 cm) x 5 cm
L = x 14 x 5
L = 35cm2
So, The area of the trapezium is = 35cm2
- If a trapezium has parallel sides that are 12 m and 32 m long and 10 m high, find and calculate the area of the trapezium!
Solution:
Is known :
parallel side = a1 = 12 m,
a2 = 32 m
t = 10 m
asked: L = …?
Answer:
L = x (a1 + a2) x t
L = x (12 m + 32 m) x 10 m
L = x 44 x 10
L = 220 m2
So, The area of the trapezium is = 220 m2
- It is known that the area of a trapezium = 104 cm2, and the lengths of the parallel sides are 15 cm and 11 cm. find and calculate the height of the trapezium!
Solution:
Is known :
a = 15 cm
b = 11 cm
L = 104 cm2
asked: t =…?
Answer:
t = 2L: (a + b)
t = 2. 104: (15 + 11)
t =208:26
t =8 cm2
So, the height of the trapezium is = 8 cm2
- It is known that the height of a trapezium = 0.9 m, and the parallel sides are 4 m and 3 m long. find and calculate the area of the trapezium!
Solution:
Is known :
a1= 4 m
b1= 3 m
t= 0.9 m
asked: L =…?
Answer:
L =½ x (a1 + b1) x t
L =½ x (4 m + 3 m) x 0.9 m
L =½ x 7 x 0.9
L =3.5 x 0.9
L =3.15 m2
So, The area of the trapezium is = 3.15 m2
5. If a trapezium has parallel sides that are 24 cm and 34 cm long and 15 cm high, find and calculate the area of the trapezium!
Solution:
Is known :
parallel side = a1 = 24 cm,
b1 = 34 cm
t = 15 cm
asked: L = …?
Answer:
L = x (a1 + a2) x t
L = x (24 cm + 34 cm) x 15 cm
L = x 58 x 15
L = 435 cm2
So, The area of the trapezium is = 435cm2
6. If a trapezium has parallel sides that are 46 cm and 31 cm long and 25 cm high, find and calculate the area of the trapezium!
Solution:
Is known :
parallel side = a1 = 46 cm,
b1 = 31 cm
t = 25 cm
asked: L = …?
Answer:
L = x (a1 + a2) x t
L = x (46 cm + 31 cm) x 25 cm
L = x 77 x 25
L = 962,5 cm2
So, The area of the trapezium is = 962,5 cm2
7. If a trapezium has parallel sides that are 29 cm and 19 cm respectively and a height of 22 cm, find and calculate the area of the trapezium!
Solution:
Is known :
parallel side = a1 = 29 cm,
b1 = 19 cm
t = 22 cm
asked: L = …?
Answer:
L = x (a1 + a2) x t
L = x (29 cm + 19 cm) x 22 cm
L = x 48 x 22
L = 528 cm2
So, The area of the trapezium is = 528 cm2
This is a complete discussion of how to calculate the trapezoidal formula along with examples of questions and discussion, hopefully it will be useful…
Also Read:
- The formula for the area of a right angled triangle
- Spherical Surface Area Formula
