√ Definition of Derivatives, Types, Formulas, & Example Problems

August 15, 2023
InLinks Policy Contact

click fraud protection

The discussion of derivatives needs to be studied. By using the limit concept that you have learned, you will easily learn the following derivative material.

Definition of Derivative

The derivative is a calculation of changes in function values due to changes in input values (variables).

The derivative can also be called differential and the process of determining the derivative of a function is called differentiation.

Using the limit concept that has been studied, the derivative can be defined as

the derivative is defined as the limit of the average change of the value of the function to variable x.

In the following, an example of the implementation of inheritance will be explained.

Derived Application

Here are some derived implementations.

The derivative can be applied to calculate the gradient of the tangent to a curve.
The derivative can be used to determine the interval over which a function increases or decreases.
Derivatives can be applied to determine the stationary value of a function.

instagram viewer

Derivatives can be applied in solving problems related to the equation of motion.
Derivatives can be used to solve maximum-minimum problems.

The following will explain the derivative formula.

Derivative Formulas

Here are some basic formulas for determining the derivative.

f(x) = c, where c is a constant

The derivative of this function is f'(x) = 0.

f(x) = x

The derivative of this function is f'(x) = 1.

f(x) = axⁿ

The derivative of this function is f'(x) = anx^n–1

Function addition: h(x) = f(x) + g(x)

The derivative of this function is h'(x) = f'(x) + g'(x).

Subtraction function: h (x) = f (x) – g (x)

The derivative of this function is h'(x) = f'(x) – g'(x)

Constant multiplication by a function (kf)(x).

The derivative of this function is k. f'(x).

In the following, we will explain the derivative function.

Function Derivation

Suppose there is a function f (x) = axⁿ. The derivative of this function is f'(x) = anx^n–1.

Examples are:

f(x) = 3x³

the derivative of the function i.e

f'(x) = 3 (3) x^{3 – 1} = 9x².

Another example is for example g (x) = -5y^-3.

The derivative of this function is g'(y) = -5 (-3) y^{-3 – 1} = 15y^-4.

The following will explain the derivative of algebraic functions.

Derivative of Algebraic Functions

The discussion on the derivatives of algebraic functions in this section includes derivatives in the form of multiplication and derivatives in the distribution of algebraic functions.

The derivative of the algebraic function in multiplication form is as follows.

Suppose there is a multiplication of functions: h (x) = u (x). v(x).

The derivative of this function is h'(x) = u'(x). v(x) + u(x). v'(x).

Information:

h(x): function in multiplication form.
h'(x): the derivative of the multiplication form function
u(x), v(x): functions with variable x
u'(x), v'(x): derivative of functions with variable x

The derivative of the algebraic function in division form is:

Suppose there is a multiplication function: h (x) = u (x)/v (x). The derivative of this function is

h'(x) = (u'(x). v(x) – u(x). v'(x))/v²(x).

Information:

h(x): function in multiplication form.
h'(x): the derivative of the multiplication form function
u(x), v(x): functions with variable x
u'(x), v'(x): derivative of functions with variable x

The following will explain about root derivatives.

Root Derivatives

Suppose there is a root function as follows

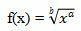
To determine the derivative of this function, we first change it to the exponential function. The exponential form of the function is f (x) = x^a/b.

The derivative of this function is f'(x) = a/b. x^{(a/b) – 1}.

What if the function looks like this?

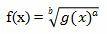
To determine the derivative of the function above, it must first be changed to exponential form.

f(x) = g(x)^z/b

The derivative of this function is f'(x) = a/b. g(x)^{(a/b) – 1}. g'(x).

The following will explain about partial derivatives.

Partial Derivative

What is a partial derivative? The partial derivative is a derivative of the function of many variables with respect to a variable, while the other variables are maintained.

Suppose there is a function: f (x, y) = 2xy, the partial derivative of the function with respect to variable x is f_x’(x, y) = 2y.

The partial derivative of the variable y is f_y’(x, y) = -6xy.

The following will explain about implicit derivatives.

Implicit Derivative

The implicit derivative is determined based on the variables contained in the function.

A function with variable x, its derivative: x d/dx.

A function with variable y, its derivative: y d/dy. dy/dx.

A function with variables x and y, derivative: xy d/dx + xy d/dy. dy/dx.

Another example is, there is a function g (x, y) = -3xy²

To better understand derivatives, try doing the following questions and then check your answers using the discussion in the section below.

Examples of Derivative Questions

1. Find the derivative of the following function.

f(x) = 8
g(x) = 3x + 5
h(x) = 6x³
k(x) = 3x^5/3
m(x) = (3x² + 3)⁴

Discussion

f'(x) = 0
g'(x) = 3
h'(x) = 6 (3) x^{3 – 1}= 18x²
k'(x) = 3 (5/3) x^{(5/3) – 1} = 5x^2/3
m'(x) = 4. (3x² + 3)^{4 – 1}. 6x = 24x. (3x² + 3)³
2. Find the derivative of the following function.
f(x) = (3x + 2). (2x² – 1)

Discussion

For example: u (x) = 3x + 2 and v (x) = 2x² – 1

f'(x) = u'(x). v(x) + u(x). v'(x)

f'(x) = 3. (2x² – 1) + (3x + 2). (4x)

f'(x) = 6x² – 3 + 12x² + 8x = 18x² +8x – 3

3. Given a function of order 2 as below

Determine the value of f (0) + 3f'(1)

Discussion

To do this problem, we can enter the value 0 into the function.

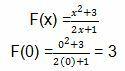
After you, get the value of f(0). We can work on the derivative of the quotient function using any of the derived properties.

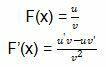
To use the formula, we can use the example and its derivatives as below.

U = x2 + 3; U' = 2x

V = 2x + 1; V' = 2

Then, we can enter this example into the previous derivative formula and we can directly enter f'x (1).

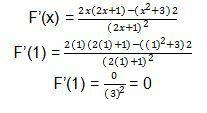
So, the result f (0) + 3f'(1) = 3 + 3(0) = 3

4. Find the derivative f (x) = (x² + 2x + 3)(3x + 2)

Discussion

Just like the previous problem, to work on the derivative problem in multiplication form, we can use the formula for the derived property and use an example in the function as below.

F'(x) = u'v + uv'

U = x² +2x +3; U' = 2x + 3

V = 3x + 2; V' = 3

F'(x) = u'v + uv'

F'(x) = (2x+3)(3x + 2) + (x² + 2x + 3)(3)

F'(x) = 6x²+13x +6 +3x²+6x+9

F'(x) = 9x² +19x +15

So the final form F'(x) is 9x² +19x +15

5. If there is f (x) = (2x-1)²(x+2). What is the value of f'x (2)
Discussion
To do this problem, we can use the derivative property of the function f'(x) = u'v + v'u to get the final result. So we can do the separation again.

F'(x) = u'v + uv'

U= (2x-1)² = 4x²– 4x + 1; U' = 8x – 4

V = x + 2; V' = 1

F'(x) = u'v + uv'

F'(x) = (8x – 4)(x + 2) + (4x²– 4x + 1)(1); we can enter the value 2 as in the problem

F'(2) = ((8(2) – 4)(2 + 2)) + ((4(2)²– 4(2) + 1)(1))

F'(2) = ((16-4)(4)) + ((16-8+1)(1))

F'(2) = 96 + 9 = 105

So that the final value of F'(2) is 105

6. Find a tangent to the curve y= -2x² + 6x + 7 which is perpendicular to the line x – 2y +13 = 0

Discussion

It is stated in the problem that there are 2 lines that are perpendicular to each other, so we can assume that the two lines have a certain slope. We can determine the value of m₁ and M₂ from both lines.

m₁is the slope of the line y= -2x² +6x+7. To find the value of m₁, can be done by deriving the function y= -2x² +6x+7.

m₁= y'(x) = -4x + 6

m₂is the slope of x – 2y +13. To find the value of m₂, we have to change the function to function y.

x – 2y +13 = 0

x + 13 = 2y

y = 0.5x + 6.5

m₂= y'(x) = 0.5

Because the two lines are perpendicular to each other, the value of m₁x m₂= -1.

m₁x m₂= -1

(-4x + 6)0.5 = -1

-2x + 3 = -1

-2x = -4

X = 2

We plug it into the equation m₁so that the value of m is obtained₁ = -2. After finding the value of x, we enter that value into the y function so that we get the value y = 11.

To make a tangent line, the formula used is (y-y₁) = m₁(x – x₁).

(y – 11) = -2 (x – 2)

Y – 11 = -2x +4

Y = -2x + 15

The tangent is y+2x-15 = 0

7. There is a box without a lid with a square base having an area of 512 cm². What is the length of the edge so that the volume has a maximum value
Discussion
In this question, it is explained that the box does not have a lid. Thus, the box consists of 4 sides and 1 base. Assume the side of the base is s and the height of the side is t. We can write the box equation as below.

512 = area of the base + 4 sides of the box

512 = s.s + 4.s.t
512 = s² + 4st
512 – s² = 4th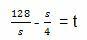

After getting t, we can find the volume of the box

V = s³ = s². t

To get the maximum volume, we can derive the volume equation above

V'(s) = 0

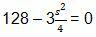
S² = 170.67 cm²

S = 13.07 cm

Thus, the length s required for the maximum volume is 13.07 cm.

The derivative is a calculation of changes in function values due to changes in input values (variables).

There are several kinds of derivatives, namely algebraic derivatives, root derivatives, partial derivatives, implicit derivatives, and others.

That's the discussion about inheritance. Hopefully it can help you in learning about derivatives. Thank You.

List of contents

Recommendation:

Validity is: Meaning and Reliability, Type,… Validity is: Definition and Reliability, Types, Principles, How to Calculate - In this review we will explain about Validity and Reliability. Which includes the understanding of the experts, types, principles of validity…
System of Two Variable Linear Inequalities System of Two Variable Linear Inequalities - Do you understand what a System of Two Variable Inequalities is all about? On this occasion, Seputarknowledge.co.id will discuss the System of Inequality of Two Variables along with things that...
Pythagoras: History, Theorem Formulas and Example Problems Pythagoras: History, Theorem Formulas and Example Problems - Who is Pythagoras with his Theorem? On this occasion, Seputarknowledge.co.id will discuss what Pythagoras is with formulas and examples the question. Let us…
√ Definition of One Variable Linear Equation (PLSV) & Examples… Definition of One Variable Linear Equation (PLSV) & Example Problems - In this discussion we will explain about one variable linear equation. Which includes the understanding of the notion of a linear equation one variable and…
Absolute Value Equation: Explanation and Example Problems Absolute Value Equations: Explanation and Example Problems - What are the properties of absolute value equations?, On On this occasion, Seputarknowledge.co.id will discuss this and of course other things as well covered it. Let's see…
Standard Deviation Formula: Definition and Example Problems Standard Deviation Formula: Definition and Example Questions - What is meant by standard deviation and how calculate using the formula? On this occasion, SeputihKnowledge.co.id will discuss the standard deviation along with…
√ Definition of Break Even Point, Formulas, Components, How to Calculate… Definition of Break Even Point, Formulas, Components, How to Calculate and Examples - In this discussion we will explain about the Break Even Point. Which includes writing, formulas, components, how to calculate and examples...
Quadratic Equations: Definition, Types, Properties, Formulas and… Quadratic Equations: Definition, Types, Properties, Formulas and Example Problems - What are quadratic equations and formulas the root? On this occasion, Seputarknowledge.co.id will discuss what is a quadratic equation, the root formula And…
Understanding the Position of Indonesian Astronomy and Its Influence… Understanding Indonesian Astronomical Positions and Their Influences (Complete) - Astronomical positions have existed since time immemorial. It's been a long time since sailors, drivers, pilots or jobs related to the location of their area determine it by…
Examples of Flat Shapes: Types, Characteristics and Formulas of Flat Shapes Examples of Flat Shapes: Types, Properties and Formulas of Flat Shapes - What are the examples of Flat Shapes?
Friendship Short Stories: Definition, Writing Tips and Examples Friendship Short Stories: Definition, Writing Tips and Examples - What are Friendship Short Stories like? On this occasion, Seputarknowledge.co.id will discuss whether it is the Short Story of Friendship and other things about it. Let's see together…
√ Definition of Electric Current, Formulas, Examples of Current Strength Problems… Definition of Electric Current Strength, Formulas, Examples of Electric Current Strength Problems - In this discussion we will explain about electric current strength. Which includes the definition of strong electric current, strong current formula…
Geometry Series: Definition, Formulas, Properties and Example Problems Geometry Series: Definition, Formulas, Properties and Example Problems - What is a geometric series?
Statistics: Definition, Scope and Formula Statistics: Definition, Scope and Formulas - What is meant by statistics? On this occasion, Seputarknowledge.co.id will discuss Statistics and its formulas. Let's look at the discussion together in the article...
Uniformly Changing Circular Motion: Definition, Magnitude… Uniformly Changing Circular Motion: Definition, Physical Quantity, Formulas and Examples of Problems - What is Motion Circular Changes Regularly and Examples? On this occasion, Seputarknowledge.co.id will discuss it and of course about...
Sharia Accounting: Understanding According to Experts, Basic… Syari'ah Accounting: Understanding According to Experts, Legal Basis, Characteristics, Purpose, Principles, Characteristics And The advantages - What is sharia accounting and its advantages? discuss it and...
√ Definition of Points, Lines and Planes (Full discussion) Definition of Points, Lines and Planes (Full discussion) - On this occasion we will discuss articles about points, lines and planes. Of course the words point, line and plane have...
Cube: Elements, Properties, Volume and Surface Area Formulas and… Cubes: Elements, Properties, Volume and Surface Area Formulas and Examples of Problems - How to calculate volume and the surface area of a cube? And…
Social Arithmetic: Overall Value, Theories and Formulas and… Social Arithmetic: Overall Value, Theory and Formulas and Example Problems - Have you understood what is meant by social arithmetic? discuss…
Moment of Inertia: Definition, Factors, Equations of Forms… Moment of Inertia: Definition, Factors, Equations in Forms of Objects and Example Problems - What is meant with the Moment of Inertia?, On this occasion, Se regarding the knowledge.co.id will discuss it and of course about matter…
√ Definition of Comparison: Kinds, Formulas, Example Problems… Definition of Comparison Comparison in mathematics can also be referred to as a ratio. Then, what is a comparison or ratio? Comparison (ratio) is a technique or way of comparing two quantities. Writing…
Vertical Downward Motion: Definition, Characteristics, Physical Quantities,… Vertical Downward Motion: Definition, Characteristics, Physical Quantities, Formulas and Example Problems - On this occasion Around the knowledge.co.id will discuss Vertical Downward Motion, formulas and of course other things Also…
Three Variable Linear Equation System: Features, Components,… System of Three Variable Linear Equations: Features, Components, Solving Methods and Example Problems - What is in what do you mean by a system of three-variable equations? On this occasion, Se regarding the knowledge.co.id will discuss it...
Badminton Game: History, Techniques, Rules, Means… Badminton Game: History, Techniques, Regulations, Facilities and Infrastructure - On this occasion About the knowledge.co.id will discuss the game of badminton and of course about other things as well covered it. Let's see…
The formula for finding the volume of a cylinder The Formula for Finding the Volume of a Cylinder - How to calculate the volume of a cylindrical shape?, On this occasion, about the knowledge.co.id will discuss it and of course other things as well covered it. Let's see together…
Compositional Functions: Formulas, Properties and Example Problems Compositional Functions: Formulas, Properties and Example Problems - What is meant by compositional functions? this time around the knowledge.co.id will discuss the function of composition and other things covered it. Let…
Flowchart: Understanding According to Experts, Purpose, Functions,… Flowchart: Understanding According to Experts, Purpose, Functions, Types and Symbols - What is meant by flowchart?, On this occasion, Seputarknowledge.co.id will discuss it and of course other things as well covered it. Let…
Arc Length Formula: Examples of Problems and Solutions Arc Length Formula: Examples of Problems and Solutions - How to measure the length of a circular arc with the formula? On this occasion, Seputarknowledge.co.id will discuss the arc length formula along with examples of problems. Let's look at the discussion together...
The Cash Flow Formula: Definition, Types and Importance of Business 2023 aroundknowledge.co.id - There is a key formula a small business owner needs to know to track incoming and outgoing cash flow. This cash flow formula will help you have enough money to not only...
Computer Hardware: How it Works, Types, Examples and… Computer Hardware: How it Works, Types, Examples and Functions - In today's computerized era, we are definitely familiar with computers and their devices. However, some may not know...